| ||||
|---|---|---|---|---|
| Cardinal | seven hundred forty-four | |||
| Ordinal | 744th (seven hundred forty-fourth) | |||
| Factorization | 23 × 3 × 31 | |||
| Divisors | 1, 2, 3, 4, 6, 8, 12, 24, 31, 62, 93, 124, 186, 248, 372, 744 | |||
| Greek numeral | ΨΜΔ´ | |||
| Roman numeral | DCCXLIV | |||
| Binary | 10111010002 | |||
| Ternary | 10001203 | |||
| Senary | 32406 | |||
| Octal | 13508 | |||
| Duodecimal | 52012 | |||
| Hexadecimal | 2E816 | |||
744 (seven hundred [and] forty four) is the natural number following 743 and preceding 745.
744 is a semiperfect number. [1] It is also an abundant number. [2] [3]
The j-invariant, an important function in the study of modular forms and Monstrous moonshine, can be written as a Fourier series in which the constant term is 744: [4] where . One consequence of this is that 744 appears in expressions for Ramanujan's constant and other almost integers.
12 (twelve) is the natural number following 11 and preceding 13. Twelve is a superior highly composite number, divisible by the numbers from 1 to 4, and 6.
70 (seventy) is the natural number following 69 and preceding 71.
90 (ninety) is the natural number following 89 and preceding 91.
24 (twenty-four) is the natural number following 23 and preceding 25. It is one sixth of a gross, or two dozens.
29 (twenty-nine) is the natural number following 28 and preceding 30. It is a prime number.
84 (eighty-four) is the natural number following 83 and preceding 85.
48 (forty-eight) is the natural number following 47 and preceding 49. It is one third of a gross, or four dozens.
63 (sixty-three) is the natural number following 62 and preceding 64.
92 (ninety-two) is the natural number following 91 and preceding 93.
104 is the natural number following 103 and preceding 105.
In mathematics, Felix Klein's j-invariant or j function, regarded as a function of a complex variable τ, is a modular function of weight zero for special linear group SL(2, Z) defined on the upper half-plane of complex numbers. It is the unique such function that is holomorphic away from a simple pole at the cusp such that
144 is the natural number following 143 and preceding 145.
4000 is the natural number following 3999 and preceding 4001. It is a decagonal number.
The Ramanujan tau function, studied by Ramanujan, is the function defined by the following identity:
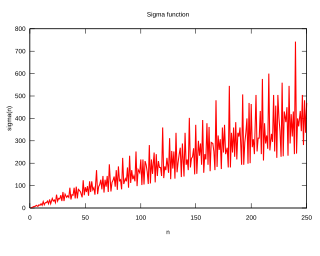
In number theory, a colossally abundant number is a natural number that, in a particular, rigorous sense, has many divisors. Particularly, it is defined by a ratio between the sum of an integer's divisors and that integer raised to a power higher than one. For any such exponent, whichever integer has the highest ratio is a colossally abundant number. It is a stronger restriction than that of a superabundant number, but not strictly stronger than that of an abundant number.
171 is the natural number following 170 and preceding 172.
1728 is the natural number following 1727 and preceding 1729. It is a dozen gross, or one great gross. It is also the number of cubic inches in a cubic foot.
240 is the natural number following 239 and preceding 241.
252 is the natural number following 251 and preceding 253.
288 is the natural number following 287 and preceding 289. Because 288 = 2 · 12 · 12, it may also be called "two gross" or "two dozen dozen".
