6

Last updated
← 5 6 7 →
−1 0 1 2 3 4 5 6 7 8 9 →
Cardinal six
Ordinal 6th
(sixth)
Numeral system senary
Factorization 2 × 3
Divisors 1, 2, 3, 6
Greek numeral Ϛ´
Roman numeral VI, vi, ↅ
Greek prefix hexa-/hex-
Latin prefix sexa-/sex-
Binary 1102
Ternary 203
Senary 106
Octal 68
Duodecimal 612
Hexadecimal 616
Greek στ (or ΣΤ or ς)
Arabic, Kurdish, Sindhi, Urdu ٦
Persian ۶
Amharic ፮
Bengali ৬
Chinese numeral 六，陸
Devanāgarī ६
Gujarati ૬
Hebrew ו
Khmer ៦
Thai ๖
Telugu ౬
Tamil ௬
Saraiki ٦
Malayalam ൬
Armenian Զ
Babylonian numeral 𒐚
Egyptian hieroglyph 𓏿
Morse code _ ....

6 (six) is the natural number following 5 and preceding 7. It is a composite number and the smallest perfect number. [1]

Contents

In mathematics

A six-sided polygon is a hexagon, [1] one of the three regular polygons capable of tiling the plane. A hexagon also has 6 edges as well as 6 internal and external angles.

6 is the second smallest composite number. [1] It is also the first number that is the sum of its proper divisors, making it the smallest perfect number. [2] 6 is the first unitary perfect number, since it is the sum of its positive proper unitary divisors, without including itself. Only five such numbers are known to exist. [3] 6 is the largest of the four all-Harshad numbers. [4]

6 is the 2nd superior highly composite number, [5] the 2nd colossally abundant number, [6] the 3rd triangular number, [7] the 4th highly composite number, [8] a pronic number, [9] a congruent number, [10] a harmonic divisor number, [11] and a semiprime. [12] 6 is also the first Granville number, or -perfect number. A Golomb ruler of length 6 is a "perfect ruler". [13]

The six exponentials theorem guarantees that under certain conditions one of a set of six exponentials is transcendental. [14] The smallest non-abelian group is the symmetric group which has 3! = 6 elements. [1] 6 the answer to the two-dimensional kissing number problem. [15]

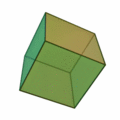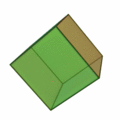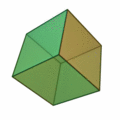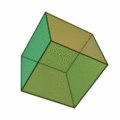
A regular cube, with six faces 120px-Hexahedron-slowturn.gif
A regular cube, with six faces

A cube has 6 faces. A tetrahedron has 6 edges. In four dimensions, there are a total of six convex regular polytopes.

In the classification of finite simple groups, twenty of twenty-six sporadic groups in the happy family are part of three families of groups which divide the order of the friendly giant, the largest sporadic group: five first generation Mathieu groups, seven second generation subquotients of the Leech lattice, and eight third generation subgroups of the friendly giant. The remaining six sporadic groups do not divide the order of the friendly giant, which are termed the pariahs (Ly, O'N, Ru, J4, J3, and J1). [16]

List of basic calculations

Multiplication 123456789101112131415161718192025501001000
6 × x6 12 18 24 30 36 42 48 54 60 66 72 78 84 90 96 102 108 114 120 150 300 600 6000
Division 123456789101112131415
6 ÷ x6321.51.210.8571420.750.60.60.540.50.4615380.4285710.4
x ÷ 60.160.30.50.60.8311.161.31.51.61.8322.162.32.5
Exponentiation 12345678109111213
6x636 216 129677764665627993616796166046617610077696362797056217678233613060694016
x61 64 72940961562546656117649262144 1000000 531441177156129859844826809

Greek and Latin word parts

Hexa

Hexa is classical Greek for "six". [1] Thus:

The prefix sex-

Sex- is a Latin prefix meaning "six". [1] Thus:

The SI prefix for 10006 is exa- (E), and for its reciprocal atto- (a).

Evolution of the Hindu-Arabic digit

The first appearance of 6 is in the Edicts of Ashoka c. 250 BCE. These are Brahmi numerals, ancestors of Hindu-Arabic numerals. Edicts of Ashoka numerals.jpg
The first appearance of 6 is in the Edicts of Ashoka c. 250 BCE. These are Brahmi numerals, ancestors of Hindu-Arabic numerals.
The first known digit "6" in the number "256" in Ashoka's Minor Rock Edict No.1 in Sasaram, c. 250 BCE Ashoka Brahmi numerals 256.jpg
The first known digit "6" in the number "256" in Ashoka's Minor Rock Edict No.1 in Sasaram, c. 250 BCE

The evolution of our modern digit 6 appears rather simple when compared with the other digits. The modern 6 can be traced back to the Brahmi numerals of India, which are first known from the Edicts of Ashoka c. 250 BCE. [23] [24] [25] [26] It was written in one stroke like a cursive lowercase e rotated 90 degrees clockwise. Gradually, the upper part of the stroke (above the central squiggle) became more curved, while the lower part of the stroke (below the central squiggle) became straighter. The Arabs dropped the part of the stroke below the squiggle. From there, the European evolution to our modern 6 was very straightforward, aside from a flirtation with a glyph that looked more like an uppercase G. [27]

On the seven-segment displays of calculators and watches, 6 is usually written with six segments. Some historical calculator models use just five segments for the 6, by omitting the top horizontal bar. This glyph variant has not caught on; for calculators that can display results in hexadecimal, a 6 that looks like a "b" is not practical.

Just as in most modern typefaces, in typefaces with text figures the character for the digit 6 usually has an ascender, as, for example, in Text figures 036.svg . [28]

This digit resembles an inverted 9. To disambiguate the two on objects and documents that can be inverted, the 6 has often been underlined, both in handwriting and on printed labels.

In music

A standard guitar has six strings. Guitar 1.jpg
A standard guitar has six strings.

In artists

In instruments

In music theory

In works

In religion

Star of David (bold).svg

Judaism

Islam

Indeed, We created the heavens and the earth and everything in between in six Days,1 and We were not ˹even˺ touched with fatigue.2

—  Surah Qaf:38

Note 1: The word day is not always used in the Quran to mean a 24-hour period. According to Surah Al-Hajj (The Pilgrimage):47, a heavenly Day is 1000 years of our time. The Day of Judgment will be 50,000 years of our time - Surah Al-Maarij (The Ascending Stairways):4. Hence, the six Days of creation refer to six eons of time, known only by Allah.

Note 2: Some Islamic scholars believe this verse comes in response to Exodus 31:17, which says, "The Lord made the heavens and the earth in six days, but on the seventh day He rested and was refreshed."

Others

In science

Astronomy

Biology

The cells of a beehive are six-sided. Bienenwabe mit Eiern und Brut 5.jpg
The cells of a beehive are six-sided.

Chemistry

A molecule of benzene has a ring of six carbon and six hydrogen atoms. Benzene structure.png
A molecule of benzene has a ring of six carbon and six hydrogen atoms.

Medicine

Physics

In the Standard Model of particle physics, there are six types of quarks and six types of leptons. Standard Model of Elementary Particles.svg
In the Standard Model of particle physics, there are six types of quarks and six types of leptons.

In technology

6 as a resin identification code, used in recycling. U+2678 DejaVu Sans.svg
6 as a resin identification code, used in recycling.

In calendars

Anthropology

See also

Related Research Articles

7 (seven) is the natural number following 6 and preceding 8. It is the only prime number preceding a cube.

In number theory, a lucky number is a natural number in a set which is generated by a certain "sieve". This sieve is similar to the sieve of Eratosthenes that generates the primes, but it eliminates numbers based on their position in the remaining set, instead of their value.

20 (twenty) is the natural number following 19 and preceding 21.

In number theory, a k-hyperperfect number is a natural number n for which the equality holds, where σ(n) is the divisor function (i.e., the sum of all positive divisors of n). A hyperperfect number is a k-hyperperfect number for some integer k. Hyperperfect numbers generalize perfect numbers, which are 1-hyperperfect.

<span class="mw-page-title-main">Quotient</span> Mathematical result of division

In arithmetic, a quotient is a quantity produced by the division of two numbers. The quotient has widespread use throughout mathematics. It has two definitions: either the integer part of a division or a fraction or ratio. For example, when dividing 20 by 3, the quotient is 6 in the first sense and in the second sense.

23 (twenty-three) is the natural number following 22 and preceding 24.

89 (eighty-nine) is the natural number following 88 and preceding 90.

34 (thirty-four) is the natural number following 33 and preceding 35.

36 (thirty-six) is the natural number following 35 and preceding 37.

37 (thirty-seven) is the natural number following 36 and preceding 38.

<span class="mw-page-title-main">360 (number)</span> Natural number

360 is the natural number following 359 and preceding 361.

<span class="mw-page-title-main">Pentagonal number</span> Figurate number

A pentagonal number is a figurate number that extends the concept of triangular and square numbers to the pentagon, but, unlike the first two, the patterns involved in the construction of pentagonal numbers are not rotationally symmetrical. The nth pentagonal number pn is the number of distinct dots in a pattern of dots consisting of the outlines of regular pentagons with sides up to n dots, when the pentagons are overlaid so that they share one vertex. For instance, the third one is formed from outlines comprising 1, 5 and 10 dots, but the 1, and 3 of the 5, coincide with 3 of the 10 – leaving 12 distinct dots, 10 in the form of a pentagon, and 2 inside.

In mathematics, the persistence of a number is the number of times one must apply a given operation to an integer before reaching a fixed point at which the operation no longer alters the number.

239 is the natural number following 238 and preceding 240.

A cyclic number is an integer for which cyclic permutations of the digits are successive integer multiples of the number. The most widely known is the six-digit number 142857, whose first six integer multiples are

257 is the natural number following 256 and preceding 258.

<span class="mw-page-title-main">Operation (mathematics)</span> Addition, multiplication, division, ...

In mathematics, an operation is a function from a set to itself. For example, an operation on real numbers will take in real numbers and return a real number. An operation can take zero or more input values to a well-defined output value. The number of operands is the arity of the operation.

In mathematics, the Golomb–Dickman constant, named after Solomon W. Golomb and Karl Dickman, is a mathematical constant, which arises in the theory of random permutations and in number theory. Its value is

Euler's "lucky" numbers are positive integers n such that for all integers k with 1 ≤ k < n, the polynomial k2 − k + n produces a prime number.

References

  1. 1 2 3 4 5 6 Weisstein, Eric W. "6". mathworld.wolfram.com. Retrieved 2020-08-03.
  2. ↑ Higgins, Peter (2008). Number Story: From Counting to Cryptography . New York: Copernicus. p.  11. ISBN   978-1-84800-000-1.
  3. ↑ Sloane, N. J. A. (ed.). "SequenceA002827(Unitary perfect numbers)". The On-Line Encyclopedia of Integer Sequences . OEIS Foundation. Retrieved 2016-06-01.
  4. ↑ Weisstein, Eric W. "Harshad Number". mathworld.wolfram.com. Retrieved 2020-08-03.
  5. ↑ "A002201 - OEIS". oeis.org. Retrieved 2024-11-28.
  6. ↑ "A004490 - OEIS". oeis.org. Retrieved 2024-11-28.
  7. ↑ "A000217 - OEIS". oeis.org. Retrieved 2024-11-28.
  8. ↑ "A002182 - OEIS". oeis.org. Retrieved 2024-11-28.
  9. ↑ "Sloane's A002378: Pronic numbers". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2020-11-30.
  10. ↑ Sloane, N. J. A. (ed.). "SequenceA003273(Congruent numbers)". The On-Line Encyclopedia of Integer Sequences . OEIS Foundation. Retrieved 2016-06-01.
  11. ↑ "A001599 - OEIS". oeis.org. Retrieved 2024-11-28.
  12. ↑ Sloane, N. J. A. (ed.). "SequenceA001358(Semiprimes (or biprimes): products of two primes.)". The On-Line Encyclopedia of Integer Sequences . OEIS Foundation. Retrieved 2023-08-03.
  13. ↑ Bryan Bunch, The Kingdom of Infinite Number. New York: W. H. Freeman & Company (2000): 72
  14. ↑ Weisstein, Eric W. "Six Exponentials Theorem". mathworld.wolfram.com. Retrieved 2020-08-03.
  15. ↑ Weisstein, Eric W. "Kissing Number". mathworld.wolfram.com. Retrieved 2020-08-03.
  16. ↑ Griess, Jr., Robert L. (1982). "The Friendly Giant" (PDF). Inventiones Mathematicae . 69: 91–96. Bibcode:1982InMat..69....1G. doi:10.1007/BF01389186. hdl:2027.42/46608. MR   0671653. S2CID   123597150. Zbl   0498.20013.
  17. ↑ Weisstein, Eric W. "Hexadecimal". mathworld.wolfram.com. Retrieved 2020-08-03.
  18. ↑ Weisstein, Eric W. "Hexagon". mathworld.wolfram.com. Retrieved 2020-08-03.
  19. ↑ Weisstein, Eric W. "Hexahedron". mathworld.wolfram.com. Retrieved 2020-08-03.
  20. ↑ Weisstein, Eric W. "Base". mathworld.wolfram.com. Retrieved 2020-08-03.
  21. ↑ Chris K. Caldwell; G. L. Honaker Jr. (2009). Prime Curios!: The Dictionary of Prime Number Trivia. CreateSpace Independent Publishing Platform. p. 11. ISBN   978-1-4486-5170-2.
  22. ↑ Weisstein, Eric W. "Sexy Primes". mathworld.wolfram.com. Retrieved 2020-08-03.
  23. ↑ Hollingdale, Stuart (2014). Makers of Mathematics. Courier Corporation. pp. 95–96. ISBN   978-0-486-17450-1.
  24. ↑ Publishing, Britannica Educational (2009). The Britannica Guide to Theories and Ideas That Changed the Modern World. Britannica Educational Publishing. p. 64. ISBN   978-1-61530-063-1.
  25. ↑ Katz, Victor J.; Parshall, Karen Hunger (2014). Taming the Unknown: A History of Algebra from Antiquity to the Early Twentieth Century. Princeton University Press. p. 105. ISBN   978-1-4008-5052-5.
  26. ↑ Pillis, John de (2002). 777 Mathematical Conversation Starters. MAA. p. 286. ISBN   978-0-88385-540-9.
  27. ↑ Georges Ifrah, The Universal History of Numbers: From Prehistory to the Invention of the Computer transl. David Bellos et al. London: The Harvill Press (1998): 395, Fig. 24.66
  28. ↑ Negru, John (1988). Computer Typesetting. Van Nostrand Reinhold. p. 59. ISBN   978-0-442-26696-7. slight ascenders that rise above the cap height ( in 4 and 6 )
  29. ↑ Auric, Georges; Durey, Louis; Honegger, Arthur; Milhaud, Darius; Poulenc, Francis; Tailleferre, Germaine (2014-08-20). Caramel Mou and Other Great Piano Works of "Les Six": Pieces by Auric, Durey, Honegger, Milhaud, Poulenc and Tailleferre (in French). Courier Corporation. ISBN   978-0-486-49340-4.
  30. ↑ "Six Organs of Admittance". www.sixorgans.com. Retrieved 2020-08-03.
  31. ↑ "Electric Six | Biography, Albums, Streaming Links". AllMusic. Retrieved 2020-08-03.
  32. ↑ "Sixpence None The Richer". GRAMMY.com. 2020-05-19. Retrieved 2020-08-04.
  33. ↑ "Slant 6 | Biography & History". AllMusic. Retrieved 2020-08-04.
  34. ↑ "You Me at Six | Biography & History". AllMusic. Retrieved 2020-08-04.
  35. ↑ "Definition of GUITAR". www.merriam-webster.com. Retrieved 2020-08-04.
  36. ↑ D'Amante, Elvo (1994-01-01). Music Fundamentals: Pitch Structures and Rhythmic Design. Scarecrow Press. p. 194. ISBN   978-1-4616-6985-2. The division of an octave into six equal parts is referred to as the whole-tone scale
  37. ↑ Horsley, Charles Edward (1876). A Text Book of Harmony: For the Use of Schools and Students. Sampson Low, Marston, Searle, & Rivington. p. 4. Like the Tritone, it contains six semitones
  38. ↑ Tribble, Mimi (2004). 300 Ways to Make the Best Christmas Ever!: Decorations, Carols, Crafts & Recipes for Every Kind of Christmas Tradition. Sterling Publishing Company, Inc. p. 145. ISBN   978-1-4027-1685-0. Six geese a-laying
  39. ↑ Staines, Joe (2010-05-17). The Rough Guide to Classical Music. Penguin. p. 393. ISBN   978-1-4053-8321-9. ...the six arias with variations collected under the title Hexachordum Apollinis (1699)...
  40. ↑ Hegarty, Paul; Halliwell, Martin (2011-06-23). Beyond and Before: Progressive Rock since the 1960s. Bloomsbury Publishing USA. p. 169. ISBN   978-1-4411-1480-8. Six Degrees of Inner Turbulence
  41. ↑ Curran, Angela (2015-10-05). Routledge Philosophy Guidebook to Aristotle and the Poetics. Routledge. p. 133. ISBN   978-1-317-67706-2. THE SIX QUALITATIVE ELEMENTS OF TRAGEDY
  42. ↑ Plaut, W. Gunther (1991). The Magen David: How the Six-pointed Star Became an Emblem for the Jewish People. B'nai B'rith Books. ISBN   978-0-910250-16-0. How the Six-pointed Star Became an Emblem for the Jewish People
  43. ↑ Lauterbach, Jacob Zallel (1916). Midrash and Mishnah: A Study in the Early History of the Halakah. Bloch. p. 9. Six orders of Mishnah
  44. ↑ Rosen, Ceil; Rosen, Moishe (2006-05-01). Christ in the Passover. Moody Publishers. p. 79. ISBN   978-1-57567-480-3. Six symbolic foods
  45. ↑ Repcheck, Jack (2008-12-15). The Man Who Found Time: James Hutton And The Discovery Of Earth's Antiquity. Basic Books. ISBN   978-0-7867-4399-5. it actually took only six days to create the earth
  46. ↑ "CHURCH FATHERS: City of God, Book XI (St. Augustine)". www.newadvent.org. Retrieved 2020-08-04. These works are recorded to have been completed in six days (the same day being six times repeated), because six is a perfect number
  47. ↑ Grossman, Grace Cohen; Ahlborn, Richard E.; Institution, Smithsonian (1997). Judaica at the Smithsonian: Cultural Politics as Cultural Model. Smithsonian Institution Press. p. 228. Shavuot falls on the sixth day of the Hebrew month of Sivan
  48. ↑ Robertson, William Archibald Scott (1880). The crypt of Canterbury cathedral; its architecture, its history, and its frescoes. Mitchell & Hughes. p. 91. ...but seraphs, with six wings
  49. ↑ Shapera, Paul M. (2009-08-15). Iran's Religious Leaders. The Rosen Publishing Group, Inc. p. 10. ISBN   978-1-4358-5283-9. Islam has six articles of faith
  50. ↑ Algül, Hüseyin (2005). The Blessed Days and Nights of the Islamic Year. Tughra Books. p. 65. ISBN   978-1-932099-93-5. ...it was blessed to fast for six days in the month of Shawwal...
  51. ↑ "Surah Qaf - 38". Quran.com. Retrieved 2023-08-28.
  52. ↑ Bary, William Theodore De; DeBary, William T.; Chan, Wing-tsit; Lufrano, Richard; Ching, Julia; Johnson, David; Liu, Kwang-Ching; Mungello, David (1999). Sources of Chinese Tradition. Columbia University Press. ISBN   978-0-231-11270-3. ...and the Six Ministries were made...
  53. ↑ Rhoads, Samuel E. (1996). The Sky Tonight: A Guided Tour of the Stars Over Hawaiʻi. Bishop Museum Press. ISBN   978-0-930897-93-2. Three Messier objects are visible in this part of the sky : M6, M7 and M8 .
  54. ↑ Sedgwick, Marcus (2011-07-05). White Crow. Roaring Brook Press. p. 145. ISBN   978-1-4299-7634-3. The cells of honeycombs are six-sided because a hexagon is the most material-efficient tessellation
  55. ↑ Parker, Steve (2005). Ant Lions, Wasps & Other Insects. Capstone. p. 16. ISBN   978-0-7565-1250-7. Insects have six legs each...
  56. ↑ Pendarvis, Murray P.; Crawley, John L. (2019-02-01). Exploring Biology in the Laboratory: Core Concepts. Morton Publishing Company. p. 10. ISBN   978-1-61731-899-3. ...presently at least six kingdoms are recognized;
  57. ↑ Mader, Sylvia S. (2004). Biology. McGraw-Hill. p. 20. ISBN   978-0-07-291934-9. The acronym CHNOPS helps us remember these six elements
  58. ↑ Dufour, Fritz (2018-09-19). The Realities of Reality - Part II: Making Sense of Why Modern Science Advances. Vol. 1. Fritz Dufour. p. 100. The benzene molecule has its six carbon atoms in a ring[ self-published source? ]
  59. ↑ Starr, Cecie; Evers, Christine (2012-05-10). Biology Today and Tomorrow without Physiology. Cengage Learning. p. 25. ISBN   978-1-133-36536-5. For example, the atomic number of carbon is 6,
  60. ↑ Webb, Stephen; Webb, Professor of Australian Studies Stephen (2004-05-25). Out of this World: Colliding Universes, Branes, Strings, and Other Wild Ideas of Modern Physics. Springer Science & Business Media. p. 16. ISBN   978-0-387-02930-6. snowflake, with its familiar sixfold rotational symmetry
  61. ↑ Woo, Teri Moser; Robinson, Marylou V. (2015-08-03). Pharmacotherapeutics For Advanced Practice Nurse Prescribers. F.A. Davis. p. 145. ISBN   978-0-8036-4581-3. Ayurvedic herbology is based on the tridoshic theory that there exist six basic tastes
  62. ↑ Pandemic Influenza Preparedness and Response Guidance for Healthcare Workers and Healthcare Employers. OSHA, U.S. Department of Labor. 2007. p. 8. The WHO Plan describes six phases of increasing public health risk associated with the emergence of a new influenza
  63. ↑ Sanghera, Paul (2011-03-08). Quantum Physics for Scientists and Technologists: Fundamental Principles and Applications for Biologists, Chemists, Computer Scientists, and Nanotechnologists. John Wiley & Sons. p. 64. ISBN   978-0-470-92269-9. ...there are six types of quarks and six types of leptons.
  64. ↑ Jimbo, M.; Jimbo, Michio; Miwa, Tetsuji; Tsuchiya, Akihiro (1989). Integrable Systems in Quantum Field Theory and Statistical Mechanics. Academic Press. p. 588. ISBN   978-0-12-385342-4. Allowed configurations in the six-vertex model and their statistical weights
  65. ↑ Sloan, Robin James Stuart (2015-05-07). Virtual Character Design for Games and Interactive Media. CRC Press. p. 34. ISBN   978-1-4665-9820-1. placing six primaries around the wheel in the following order: red, yellow, green, cyan, blue, magenta.
  66. ↑ Stevens, E. S. (2002). Green Plastics: An Introduction to the New Science of Biodegradable Plastics. Princeton University Press. p. 45. ISBN   978-0-691-04967-0.
  67. ↑ Bunson, Matthew (2014-05-14). Encyclopedia of the Roman Empire. Infobase Publishing. p. 90. ISBN   978-1-4381-1027-1. Augustus was also originally called Sextilis, the sixth month.
  68. ↑ Nicolas, Sir Nicholas Harris (1833). The Chronology of History: Containing Tables, Calculations and Statements, Indispensable for Ascertaining the Dates of Historical Events and of Public and Private Documents from the Earliest Period to the Present Time. Longham, Rees, Orme, Brown, Green, & Longman and John Taylor. p. 172. SEXTIDI, or " Jour de la Révolution, "
  69. ↑ Rimes, Wendy (2016-04-01). "The Reason Why The Dead Are Buried Six Feet Below The Ground". Elite Readers. Retrieved 2020-08-06.
  70. ↑ "Six Degrees of Peggy Bacon". www.aaa.si.edu. 27 June 2012. Retrieved 2020-08-06.
  71. ↑ "Virgo | constellation and astrological sign". Encyclopedia Britannica. Retrieved 2020-08-06.
  72. ↑ Wilkinson, Endymion Porter; Wilkinson, Scholar and Diplomat (Eu Ambassador to China 1994-2001) Endymion (2000). Chinese History: A Manual. Harvard Univ Asia Center. p. 11. ISBN   978-0-674-00249-4.{{cite book}}: CS1 maint: numeric names: authors list (link)
  73. ↑ Peirce, Gareth (2011-03-12). "The Birmingham Six: Have we learned from our disgraceful past?". The Guardian. ISSN   0261-3077 . Retrieved 2020-08-06.
  74. ↑ Smith, Michael (2011-10-31). Six: The Real James Bonds 1909-1939. Biteback Publishing. ISBN   978-1-84954-264-7.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.