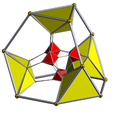
Cantic 6-cube

Cantic 6-cube Truncated 6-demicube
D6 Coxeter plane projection
Type	uniform polypeton
Schläfli symbol	t0,1{3,33,1} h2{4,34}
Coxeter-Dynkin diagram	=
5-faces	76
4-faces	636
Cells	2080
Faces	3200
Edges	2160
Vertices	480
Vertex figure	( )v[{ }x{3,3}]
Coxeter groups	D6, [33,1,1]
Properties	convex

In six-dimensional geometry, a cantic 6-cube (or a truncated 6-demicube) is a uniform 6-polytope.

Alternate names

• Truncated 6-demicube
• Truncaced demihexeract
• Truncated hemihexeract (Acronym: thax) (Jonathan Bowers) ^[1]

Cartesian coordinates

The Cartesian coordinates for the 480 vertices of a cantic 6-cube centered at the origin and edge length 6√2 are coordinate permutations:

(±1,±1,±3,±3,±3,±3)

with an odd number of plus signs.

Images

orthographic projections

Coxeter plane	B6
Graph
Dihedral symmetry	[12/2]
Coxeter plane	D6	D5
Graph
Dihedral symmetry	[10]	[8]
Coxeter plane	D4	D3
Graph
Dihedral symmetry	[6]	[4]
Coxeter plane	A5	A3
Graph
Dihedral symmetry	[6]	[4]

Related polytopes

Dimensional family of cantic n-cubes

n	3	4	5	6	7	8
Symmetry [1+,4,3n-2]	[1+,4,3] = [3,3]	[1+,4,32] = [3,31,1]	[1+,4,33] = [3,32,1]	[1+,4,34] = [3,33,1]	[1+,4,35] = [3,34,1]	[1+,4,36] = [3,35,1]
Cantic figure
Coxeter	=	=	=	=	=	=
Schläfli	h2{4,3}	h2{4,32}	h2{4,33}	h2{4,34}	h2{4,35}	h2{4,36}

There are 47 uniform polytopes with D₆ symmetry, 31 are shared by the B₆ symmetry, and 16 are unique:

D6 polytopes
h{4,34}	h2{4,34}	h3{4,34}	h4{4,34}	h5{4,34}	h2,3{4,34}	h2,4{4,34}	h2,5{4,34}
h3,4{4,34}	h3,5{4,34}	h4,5{4,34}	h2,3,4{4,34}	h2,3,5{4,34}	h2,4,5{4,34}	h3,4,5{4,34}	h2,3,4,5{4,34}

Notes

1. Klitzing, (x3x3o *b3o3o3o – thax).

References

• H.S.M. Coxeter:
  • H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
  • Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, wiley.com, ISBN   978-0-471-01003-6
    • (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
    • (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
    • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
• Norman Johnson Uniform Polytopes, Manuscript (1991)
  • N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D.
• Klitzing, Richard. "6D uniform polytopes (polypeta) with acronyms". x3x3o *b3o3o3o – thax

External links

• Polytopes of Various Dimensions
• Multi-dimensional Glossary

v t e Fundamental convex regular and uniform polytopes in dimensions 2–10
Family	An	Bn	I2(p) / Dn	E6 / E7 / E8 / F4 / G2	Hn
Regular polygon	Triangle	Square	p-gon	Hexagon	Pentagon
Uniform polyhedron	Tetrahedron	Octahedron • Cube	Demicube		Dodecahedron • Icosahedron
Uniform polychoron	Pentachoron	16-cell • Tesseract	Demitesseract	24-cell	120-cell • 600-cell
Uniform 5-polytope	5-simplex	5-orthoplex • 5-cube	5-demicube
Uniform 6-polytope	6-simplex	6-orthoplex • 6-cube	6-demicube	122 • 221
Uniform 7-polytope	7-simplex	7-orthoplex • 7-cube	7-demicube	132 • 231 • 321
Uniform 8-polytope	8-simplex	8-orthoplex • 8-cube	8-demicube	142 • 241 • 421
Uniform 9-polytope	9-simplex	9-orthoplex • 9-cube	9-demicube
Uniform 10-polytope	10-simplex	10-orthoplex • 10-cube	10-demicube
Uniform n-polytope	n-simplex	n-orthoplex • n-cube	n-demicube	1k2 • 2k1 • k21	n-pentagonal polytope
Topics: Polytope families • Regular polytope • List of regular polytopes and compounds