Cantic 7-cube

Cantic 7-cube Truncated 7-demicube
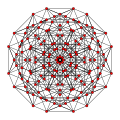
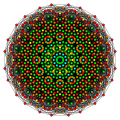
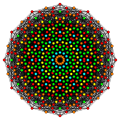
D7 Coxeter plane projection
Type	uniform 7-polytope
Schläfli symbol	t{3,34,1} h2{4,3,3,3,3,3}
Coxeter diagram
6-faces	14 truncated 6-demicubes 64 truncated 6-simplexes 64 rectified 6-simplexes
5-faces	84 truncated 5-demicubes 448 truncated 5-simplexes 448 rectified 5-simplexes 448 5-simplexes
4-faces	280 truncated 16-cells 1344 truncated 5-cells 1344 rectified 5-cells 2688 5-cells
Cells	560 truncated tetrahedra 2240 truncated tetrahedra 2240 octahedra 6720 tetrahedra
Faces	2240 hexagons 2240 triangles 8960 triangles
Edges	672 segments 6720 segments
Vertices	1344
Vertex figure	( )v{ }x{3,3,3}
Coxeter groups	D7, [34,1,1]
Properties	convex

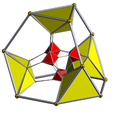
In seven-dimensional geometry, a cantic 7-cube or truncated 7-demicube as a uniform 7-polytope, being a truncation of the 7-demicube.

A uniform 7-polytope is vertex-transitive and constructed from uniform 6-polytope facets, and can be represented a coxeter diagram with ringed nodes representing active mirrors. A demihypercube is an alternation of a hypercube.

Its 3-dimensional analogue would be a truncated tetrahedron (truncated 3-demicube), and Coxeter diagram or as a cantic cube.

Alternate names

• Truncated demihepteract
• Truncated hemihepteract (acronym: thesa) (Jonathan Bowers) ^[1]

Cartesian coordinates

The Cartesian coordinates for the 1344 vertices of a truncated 7-demicube centered at the origin and edge length 6√2 are coordinate permutations:

(±1,±1,±3,±3,±3,±3,±3)

with an odd number of plus signs.

Images

It can be visualized as a 2-dimensional orthogonal projections, for example the a D₇ Coxeter plane, containing 12-gonal symmetry. Most visualizations in symmetric projections will contain overlapping vertices, so the colors of the vertices are changed based on how many vertices are at each projective position, here shown with red color for no overlaps.

orthographic projections

Coxeter plane	B7	D7	D6
Graph
Dihedral symmetry	[14/2]	[12]	[10]
Coxeter plane	D5	D4	D3
Graph
Dihedral symmetry	[8]	[6]	[4]
Coxeter plane	A5	A3
Graph
Dihedral symmetry	[6]	[4]

Related polytopes

Dimensional family of cantic n-cubes

n	3	4	5	6	7	8
Symmetry [1+,4,3n-2]	[1+,4,3] = [3,3]	[1+,4,32] = [3,31,1]	[1+,4,33] = [3,32,1]	[1+,4,34] = [3,33,1]	[1+,4,35] = [3,34,1]	[1+,4,36] = [3,35,1]
Cantic figure
Coxeter	=	=	=	=	=	=
Schläfli	h2{4,3}	h2{4,32}	h2{4,33}	h2{4,34}	h2{4,35}	h2{4,36}

There are 95 uniform polytopes with D₆ symmetry, 63 are shared by the B₆ symmetry, and 32 are unique:

D7 polytopes
t0(141)	t0,1(141)	t0,2(141)	t0,3(141)	t0,4(141)	t0,5(141)	t0,1,2(141)	t0,1,3(141)
t0,1,4(141)	t0,1,5(141)	t0,2,3(141)	t0,2,4(141)	t0,2,5(141)	t0,3,4(141)	t0,3,5(141)	t0,4,5(141)
t0,1,2,3(141)	t0,1,2,4(141)	t0,1,2,5(141)	t0,1,3,4(141)	t0,1,3,5(141)	t0,1,4,5(141)	t0,2,3,4(141)	t0,2,3,5(141)
t0,2,4,5(141)	t0,3,4,5(141)	t0,1,2,3,4(141)	t0,1,2,3,5(141)	t0,1,2,4,5(141)	t0,1,3,4,5(141)	t0,2,3,4,5(141)	t0,1,2,3,4,5(141)

Notes

1. Klitzing, (x3x3o *b3o3o3o3o - thesa).

References

• H.S.M. Coxeter:
  • H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover, New York, 1973
  • Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, wiley.com, ISBN   978-0-471-01003-6
    • (Paper 22) H.S.M. Coxeter, Regular and Semi-Regular Polytopes I, [Math. Zeit. 46 (1940) 380–407, MR 2,10]
    • (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559–591]
    • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3–45]
• Norman Johnson Uniform Polytopes, Manuscript (1991)
  • N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D.
• Klitzing, Richard. "7D uniform polytopes (polyexa) with acronyms". x3x3o *b3o3o3o3o – thesa

External links

• Weisstein, Eric W. "Hypercube". MathWorld .
• Polytopes of Various Dimensions
• Multi-dimensional Glossary

v t e Fundamental convex regular and uniform polytopes in dimensions 2–10
Family	An	Bn	I2(p) / Dn	E6 / E7 / E8 / F4 / G2	Hn
Regular polygon	Triangle	Square	p-gon	Hexagon	Pentagon
Uniform polyhedron	Tetrahedron	Octahedron • Cube	Demicube		Dodecahedron • Icosahedron
Uniform polychoron	Pentachoron	16-cell • Tesseract	Demitesseract	24-cell	120-cell • 600-cell
Uniform 5-polytope	5-simplex	5-orthoplex • 5-cube	5-demicube
Uniform 6-polytope	6-simplex	6-orthoplex • 6-cube	6-demicube	122 • 221
Uniform 7-polytope	7-simplex	7-orthoplex • 7-cube	7-demicube	132 • 231 • 321
Uniform 8-polytope	8-simplex	8-orthoplex • 8-cube	8-demicube	142 • 241 • 421
Uniform 9-polytope	9-simplex	9-orthoplex • 9-cube	9-demicube
Uniform 10-polytope	10-simplex	10-orthoplex • 10-cube	10-demicube
Uniform n-polytope	n-simplex	n-orthoplex • n-cube	n-demicube	1k2 • 2k1 • k21	n-pentagonal polytope
Topics: Polytope families • Regular polytope • List of regular polytopes and compounds • Polytope operations