Hyperfocal distance

Last updated December 12, 2023

In optics and photography, hyperfocal distance is a distance from a lens beyond which all objects can be brought into an "acceptable" focus. As the hyperfocal distance is the focus distance giving the maximum depth of field, it is the most desirable distance to set the focus of a fixed-focus camera.^[1] The hyperfocal distance is entirely dependent upon what level of sharpness is considered to be acceptable.

The hyperfocal distance has a property called "consecutive depths of field", where a lens focused at an object whose distance from the lens is at the hyperfocal distance $H$ will hold a depth of field from $H /2$ to infinity, if the lens is focused to $H /2$ , the depth of field will be from $H /3$ to $H$ ; if the lens is then focused to $H /3$ , the depth of field will be from $H /4$ to $H /2$ , etc.

Thomas Sutton and George Dawson first wrote about hyperfocal distance (or "focal range") in 1867.^[2] Louis Derr in 1906 may have been the first to derive a formula for hyperfocal distance. Rudolf Kingslake wrote in 1951 about the two methods of measuring hyperfocal distance.

Some cameras have their hyperfocal distance marked on the focus dial. For example, on the Minox LX focusing dial there is a red dot between 2 m and infinity; when the lens is set at the red dot, that is, focused at the hyperfocal distance, the depth of field stretches from 2 m to infinity. Some lenses have markings indicating the hyperfocal range for specific f-stops.

Two methods

There are two common methods of defining and measuring hyperfocal distance, leading to values that differ only slightly. The distinction between the two meanings is rarely made, since they have almost identical values. The value computed according to the first definition exceeds that from the second by just one focal length.

Definition 1: The hyperfocal distance is the closest distance at which a lens can be focused while keeping objects at infinity acceptably sharp. When the lens is focused at this distance, all objects at distances from half of the hyperfocal distance out to infinity will be acceptably sharp.
Definition 2: The hyperfocal distance is the distance beyond which all objects are acceptably sharp, for a lens focused at infinity.

Acceptable sharpness

The hyperfocal distance is entirely dependent upon what level of sharpness is considered to be acceptable. The criterion for the desired acceptable sharpness is specified through the circle of confusion (CoC) diameter limit. This criterion is the largest acceptable spot size diameter that an infinitesimal point is allowed to spread out to on the imaging medium (film, digital sensor, etc.).

Formulae

For the first definition,

H={\frac {f^{2}}{Nc}}+f

where

$H$ is the hyperfocal distance;
$f$ is the focal length of the lens;
$N$ is f-number ( $f/D$ for aperture diameter $D$ ); and
$c$ is the circle of confusion limit.

For any practical f-number, the added focal length is insignificant in comparison with the first term, so that

H\approx {\frac {f^{2}}{Nc}}\,.

This formula is exact for the second definition, if $H$ is measured from a thin lens, or from the front principal plane of a complex lens; it is also exact for the first definition if $H$ is measured from a point that is one focal length in front of the front principal plane. For practical purposes, there is little difference between the first and second definitions.

Derivation using geometric optics

The following derivations refer to the accompanying figures. For clarity, half the aperture and circle of confusion are indicated.^[3]

Definition 1

An object at distance $H$ forms a sharp image at distance $x$ (blue line). Here, objects at infinity have images with a circle of confusion indicated by the brown ellipse where the upper red ray through the focal point intersects the blue line.

First using similar triangles hatched in green,

{\begin{array}{crcl}&{\dfrac {x-f}{c/2}}&=&{\dfrac {f}{D/2}}\\\therefore &x-f&=&{\dfrac {cf}{D}}\\\therefore &x&=&f+{\dfrac {cf}{D}}\end{array}}

Then using similar triangles dotted in purple,

{\begin{array}{crclcl}&{\dfrac {H}{D/2}}&=&{\dfrac {x}{c/2}}\\\therefore &H&=&{\dfrac {Dx}{c}}&=&{\dfrac {D}{c}}{\Big (}f+{\dfrac {cf}{D}}{\Big )}\\&&=&{\dfrac {Df}{c}}+f&=&{\dfrac {f^{2}}{Nc}}+f\end{array}}

as found above.

Definition 2

Objects at infinity form sharp images at the focal length $f$ (blue line). Here, an object at $H$ forms an image with a circle of confusion indicated by the brown ellipse where the lower red ray converging to its sharp image intersects the blue line.

Using similar triangles shaded in yellow,

{\begin{array}{crclcl}&{\dfrac {H}{D/2}}&=&{\dfrac {f}{c/2}}\\\therefore &H&=&{\dfrac {Df}{c}}&=&{\dfrac {f^{2}}{Nc}}\end{array}}

Example

Depths of field of 3 ideal lenses of focal lengths,

f 1

,

f 2

and

f 3

, and f-numbers

N 1

,

N 2

, and

N 3

when focused at objects at different distances.

H 1

,

H 2

, and

H #

denote their respective hyperfocal distances (using Definition 1 in that article) with a circle of confusion of 0.03 mm diameter. The darker bars show how that, for fixed subject distance, the depth of field is increased by using a shorter focal length or smaller aperture. The second topmost bar of each set illustrates the configuration for a fixed focus camera with the focus permanently set at the hyperfocal distance to maximise the depth of field.

As an example, for a 50 mm lens at f/8 using a circle of confusion of 0.03 mm, which is a value typically used in 35 mm photography, the hyperfocal distance according to Definition 1 is

H={\frac {(50)^{2}}{(8)(0.03)}}+(50)=10467{\mbox{ mm}}

If the lens is focused at a distance of 10.5 m, then everything from half that distance (5.2 m) to infinity will be acceptably sharp in our photograph. With the formula for the Definition 2, the result is 10417 mm, a difference of 0.5%.

Consecutive depths of field

The hyperfocal distance has a curious property: while a lens focused at $H$ will hold a depth of field from $H /2$ to infinity, if the lens is focused to $H /2$ , the depth of field will extend from $H /3$ to $H$ ; if the lens is then focused to $H /3$ , the depth of field will extend from $H /4$ to $H /2$ . This continues on through all successive neighboring terms in the harmonic series ( $1/ x$ ) values of the hyperfocal distance. That is, focusing at $H / n$ will cause the depth of field to extend from $H /(n + 1)$ to $H /(n - 1)$ .

C. Welborne Piper calls this phenomenon "consecutive depths of field" and shows how to test the idea easily. This is also among the earliest of publications to use the word hyperfocal.^[4]

History

The concepts of the two definitions of hyperfocal distance have a long history, tied up with the terminology for depth of field, depth of focus, circle of confusion, etc. Here are some selected early quotations and interpretations on the topic.

Sutton and Dawson 1867

Thomas Sutton and George Dawson define focal range for what we now call hyperfocal distance:^[2]

Focal Range. In every lens there is, corresponding to a given apertal ratio (that is, the ratio of the diameter of the stop to the focal length), a certain distance of a near object from it, between which and infinity all objects are in equally good focus. For instance, in a single view lens of 6 inch focus, with a 1/4 in. stop (apertal ratio one-twenty-fourth), all objects situated at distances lying between 20 feet from the lens and an infinite distance from it (a fixed star, for instance) are in equally good focus. Twenty feet is therefore called the "focal range" of the lens when this stop is used. The focal range is consequently the distance of the nearest object, which will be in good focus when the ground glass is adjusted for an extremely distant object. In the same lens, the focal range will depend upon the size of the diaphragm used, while in different lenses having the same apertal ratio the focal ranges will be greater as the focal length of the lens is increased. The terms 'apertal ratio' and 'focal range' have not come into general use, but it is very desirable that they should, in order to prevent ambiguity and circumlocution when treating of the properties of photographic lenses. 'Focal range' is a good term, because it expresses the range within which it is necessary to adjust the focus of the lens to objects at different distances from it – in other words, the range within which focusing becomes necessary.

Their focal range is about 1000 times their aperture diameter, so it makes sense as a hyperfocal distance with CoC value of f/1000, or image format diagonal times 1/1000 assuming the lens is a "normal" lens. What is not clear, however, is whether the focal range they cite was computed, or empirical.

Abney 1881

Sir William de Wivelesley Abney says:^[5]

The annexed formula will approximately give the nearest point $p$ which will appear in focus when the distance is accurately focussed, supposing the admissible disc of confusion to be 0.025 cm:
$p=0.41\cdot f^{2}\cdot a$
when
$f =$ the focal length of the lens in cm
$a =$ the ratio of the aperture to the focal length

That is, $a$ is the reciprocal of what we now call the f-number, and the answer is evidently in meters. His 0.41 should obviously be 0.40. Based on his formulae, and on the notion that the aperture ratio should be kept fixed in comparisons across formats, Abney says:

It can be shown that an enlargement from a small negative is better than a picture of the same size taken direct as regards sharpness of detail. ... Care must be taken to distinguish between the advantages to be gained in enlargement by the use of a smaller lens, with the disadvantages that ensue from the deterioration in the relative values of light and shade.

Taylor 1892

John Traill Taylor recalls this word formula for a sort of hyperfocal distance:^[6]

We have seen it laid down as an approximative rule by some writers on optics (Thomas Sutton, if we remember aright), that if the diameter of the stop be a fortieth part of the focus of the lens, the depth of focus will range between infinity and a distance equal to four times as many feet as there are inches in the focus of the lens.

This formula implies a stricter CoC criterion than we typically use today.

Hodges 1895

John Hodges discusses depth of field without formulas but with some of these relationships:^[7]

There is a point, however, beyond which everything will be in pictorially good definition, but the longer the focus of the lens used, the further will the point beyond which everything is in sharp focus be removed from the camera. Mathematically speaking, the amount of depth possessed by a lens varies inversely as the square of its focus.

This "mathematically" observed relationship implies that he had a formula at hand, and a parameterization with the f-number or "intensity ratio" in it. To get an inverse-square relation to focal length, you have to assume that the CoC limit is fixed and the aperture diameter scales with the focal length, giving a constant f-number.

Piper 1901

C. Welborne Piper may be the first to have published a clear distinction between Depth of Field in the modern sense and Depth of Definition in the focal plane, and implies that Depth of Focus and Depth of Distance are sometimes used for the former (in modern usage, Depth of Focus is usually reserved for the latter).^[4] He uses the term Depth Constant for $H$ , and measures it from the front principal focus (i. e., he counts one focal length less than the distance from the lens to get the simpler formula), and even introduces the modern term:

This is the maximum depth of field possible, and $H + f$ may be styled the distance of maximum depth of field. If we measure this distance extra-focally it is equal to $H$ , and is sometimes called the hyperfocal distance. The depth constant and the hyperfocal distance are quite distinct, though of the same value.

It is unclear what distinction he means. Adjacent to Table I in his appendix, he further notes:

If we focus on infinity, the constant is the focal distance of the nearest object in focus. If we focus on an extra-focal distance equal to the constant, we obtain a maximum depth of field from approximately half the constant distance up to infinity. The constant is then the hyper-focal distance.

At this point we do not have evidence of the term hyperfocal before Piper, nor the hyphenated hyper-focal which he also used, but he obviously did not claim to coin this descriptor himself.

Derr 1906

Louis Derr may be the first to clearly specify the first definition,^[8] which is considered to be the strictly correct one in modern times, and to derive the formula corresponding to it. Using $p$ for hyperfocal distance, $D$ for aperture diameter, $d$ for the diameter that a circle of confusion shall not exceed, and $f$ for focal length, he derives:^[9]

p={\frac {(D+d)f}{d}}\,.

As the aperture diameter, $D$ is the ratio of the focal length $f$ to the numerical aperture $N$ ( $D = f / N$ ); and the diameter of the circle of confusion, $c = d$ , this gives the equation for the first definition above.

p={\frac {\left({\tfrac {f}{N}}+c\right)f}{c}}={\frac {f^{2}}{Nc}}+f

Johnson 1909

George Lindsay Johnson uses the term Depth of Field for what Abney called Depth of Focus, and Depth of Focus in the modern sense (possibly for the first time),^[10] as the allowable distance error in the focal plane. His definitions include hyperfocal distance:

Depth of Focus is a convenient, but not strictly accurate term, used to describe the amount of racking movement (forwards or backwards) which can be given to the screen without the image becoming sensibly blurred, i.e. without any blurring in the image exceeding 1/100 in., or in the case of negatives to be enlarged or scientific work, the 1/10 or 1/100*nbsp;mm. Then the breadth of a point of light, which, of course, causes blurring on both sides, i.e. {{{1}}} (or {{{1}}}).

His drawing makes it clear that his $e$ is the radius of the circle of confusion. He has clearly anticipated the need to tie it to format size or enlargement, but has not given a general scheme for choosing it.

Depth of Field is precisely the same as depth of focus, only in the former case the depth is measured by the movement of the plate, the object being fixed, while in the latter case the depth is measured by the distance through which the object can be moved without the circle of confusion exceeding 2 $e$ .
Thus if a lens which is focused for infinity still gives a sharp image for an object at 6 yards, its depth of field is from infinity to 6 yards, every object beyond 6 yards being in focus.
This distance (6 yards) is termed the hyperfocal distance of the lens, and any allowable confusion disc depends on the focal length of the lens and on the stop used.
If the limit of confusion of half of the disc (i.e. $e$ ) be taken as 1/100 in., then the hyperfocal distance
$H={\frac {Fd}{e}}\,,$
$d$ being the diameter of the stop, ...

Johnson's use of former and latter seem to be swapped; perhaps former was here meant to refer to the immediately preceding section title Depth of Focus, and latter to the current section title Depth of Field. Except for an obvious factor-of-2 error in using the ratio of stop diameter to CoC radius, this definition is the same as Abney's hyperfocal distance.

Others, early twentieth century

The term hyperfocal distance also appears in Cassell's Cyclopaedia of 1911, The Sinclair Handbook of Photography of 1913, and Bayley's The Complete Photographer of 1914.

Kingslake 1951

Rudolf Kingslake is explicit about the two meanings:^[1]

if the camera is focused on a distance $s$ equal to 1000 times the diameter of the lens aperture, then the far depth $D 1$ becomes infinite. This critical object distance " $h$ " is known as the Hyperfocal Distance. For a camera focused on this distance, $D 1 = \infty$ and $D 2 = h /2$ , and we see that the range of distances acceptably in focus will run from just half the hyperfocal distance to infinity. The hyperfocal distance is, therefore, the most desirable distance on which to pre-set the focus of a fixed-focus camera. It is worth noting, too, that if a camera is focused on $s = \infty$ , the closest acceptable object is at $L 2 = sh /(h + s) = h /(h / s + 1) = h$ (by equation 21). This is a second important meaning of the hyperfocal distance.

Kingslake uses the simplest formulae for DOF near and far distances, which has the effect of making the two different definitions of hyperfocal distance give identical values.

Related Research Articles

In optics, aberration is a property of optical systems, such as lenses, that causes light to be spread out over some region of space rather than focused to a point. Aberrations cause the image formed by a lens to be blurred or distorted, with the nature of the distortion depending on the type of aberration. Aberration can be defined as a departure of the performance of an optical system from the predictions of paraxial optics. In an imaging system, it occurs when light from one point of an object does not converge into a single point after transmission through the system. Aberrations occur because the simple paraxial theory is not a completely accurate model of the effect of an optical system on light, rather than due to flaws in the optical elements.

<span class="mw-page-title-main">Depth of field</span> Distance between the nearest and the furthest objects that are in focus in an image

The depth of field (DOF) is the distance between the nearest and the furthest objects that are in acceptably sharp focus in an image captured with a camera.

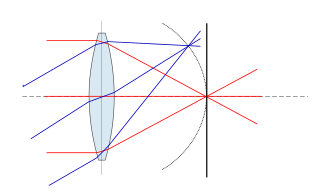
In optics, the numerical aperture (NA) of an optical system is a dimensionless number that characterizes the range of angles over which the system can accept or emit light. By incorporating index of refraction in its definition, NA has the property that it is constant for a beam as it goes from one material to another, provided there is no refractive power at the interface. The exact definition of the term varies slightly between different areas of optics. Numerical aperture is commonly used in microscopy to describe the acceptance cone of an objective, and in fiber optics, in which it describes the range of angles within which light that is incident on the fiber will be transmitted along it.

In optics, an aperture is a hole or an opening through which light travels. More specifically, the aperture and focal length of an optical system determine the cone angle of the bundle of rays that come to a focus in the image plane.

<span class="mw-page-title-main">Pinhole camera</span> Type of camera

A pinhole camera is a simple camera without a lens but with a tiny aperture —effectively a light-proof box with a small hole in one side. Light from a scene passes through the aperture and projects an inverted image on the opposite side of the box, which is known as the camera obscura effect. The size of the images depends on the distance between the object and the pinhole.

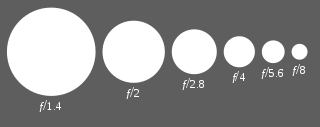
An f-number is a measure of the light-gathering ability of an optical system such as a camera lens. It is calculated by dividing the system's focal length by the diameter of the entrance pupil. The f-number is also known as the focal ratio, f-ratio, or f-stop, and it is key in determining the depth of field, diffraction, and exposure of a photograph. The f-number is dimensionless and is usually expressed using a lower-case hooked f with the format f/N, where N is the f-number.

In optics, a circle of confusion (CoC) is an optical spot caused by a cone of light rays from a lens not coming to a perfect focus when imaging a point source. It is also known as disk of confusion, circle of indistinctness, blur circle, or blur spot.

In photography, angle of view (AOV) describes the angular extent of a given scene that is imaged by a camera. It is used interchangeably with the more general term field of view.

An optical telescope is a telescope that gathers and focuses light mainly from the visible part of the electromagnetic spectrum, to create a magnified image for direct visual inspection, to make a photograph, or to collect data through electronic image sensors.

$<span class="mw-page-title-main">Airy disk</span> Diffraction pattern in optics$

In optics, the Airy disk and Airy pattern are descriptions of the best-focused spot of light that a perfect lens with a circular aperture can make, limited by the diffraction of light. The Airy disk is of importance in physics, optics, and astronomy.

Magnification is the process of enlarging the apparent size, not physical size, of something. This enlargement is quantified by a size ratio called optical magnification. When this number is less than one, it refers to a reduction in size, sometimes called de-magnification.

The Scheimpflug principle is a description of the geometric relationship between the orientation of the plane of focus, the lens plane, and the image plane of an optical system when the lens plane is not parallel to the image plane. It is applicable to the use of some camera movements on a view camera. It is also the principle used in corneal pachymetry, the mapping of corneal topography, done prior to refractive eye surgery such as LASIK, and used for early detection of keratoconus. The principle is named after Austrian army Captain Theodor Scheimpflug, who used it in devising a systematic method and apparatus for correcting perspective distortion in aerial photographs, although Captain Scheimpflug himself credits Jules Carpentier with the rule, thus making it an example of Stigler's law of eponymy.

The science of photography is the use of chemistry and physics in all aspects of photography. This applies to the camera, its lenses, physical operation of the camera, electronic camera internals, and the process of developing film in order to take and develop pictures properly.

Depth of focus is a lens optics concept that measures the tolerance of placement of the image plane in relation to the lens. In a camera, depth of focus indicates the tolerance of the film's displacement within the camera and is therefore sometimes referred to as "lens-to-film tolerance".

The EF 50mm lenses are a group of normal prime lenses made by Canon that share the same focal length. These lenses are based on the classic double-Gauss lens, with the f/1.8 being a standard six-element double-Gauss with an air gap and powers between element 2 and 3 and its faster cousins adding additional elements. The 50mm focal length, when used with a 35mm film or full-frame sensor, has been widely considered to match the perspective seen by the human eye.

The following are common definitions related to the machine vision field.

A photographic lens for which the focus is not adjustable is called a fixed-focus lens or sometimes focus-free. The focus is set at the time of lens design, and remains fixed. It is usually set to the hyperfocal distance, so that the depth of field ranges all the way down from half that distance to infinity, which is acceptable for most cameras used for capturing images of humans or objects larger than a meter.

<span class="mw-page-title-main">Tilted plane focus</span>

Tilted plane photography is a method of employing focus as a descriptive, narrative or symbolic artistic device. It is distinct from the more simple uses of selective focus which highlight or emphasise a single point in an image, create an atmospheric bokeh, or miniaturise an obliquely-viewed landscape. In this method the photographer is consciously using the camera to focus on several points in the image at once while de-focussing others, thus making conceptual connections between these points.

For digital image processing, the Focus recovery from a defocused image is an ill-posed problem since it loses the component of high frequency. Most of the methods for focus recovery are based on depth estimation theory. The Linear canonical transform (LCT) gives a scalable kernel to fit many well-known optical effects. Using LCTs to approximate an optical system for imaging and inverting this system, theoretically permits recovery of a defocused image.

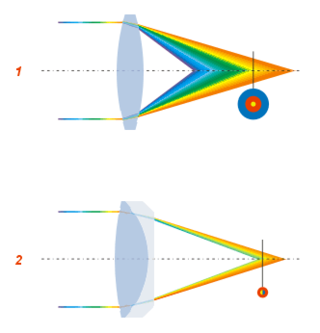
Petzval field curvature, named for Joseph Petzval, describes the optical aberration in which a flat object normal to the optical axis cannot be brought properly into focus on a flat image plane. Field curvature can be corrected with the use of a field flattener, designs can also incorporate a curved focal plane like in the case of the human eye in order to improve image quality at the focal surface.

References

1 2 Kingslake, Rudolf (1951). Lenses in Photography: The Practical Guide to Optics for Photographers. Garden City, NY: Garden City Press.
1 2 Sutton, Thomas; Dawson, George (1867). A Dictionary of Photography. London: Sampson Low, Son & Marston.
↑ Kingslake, Rudolf (1992). Optics in Photography - Google Books. ISBN 9780819407634 . Retrieved 24 September 2014.
1 2 Piper, C. Welborne (1901). A First Book of the Lens: An Elementary Treatise on the Action and Use of the Photographic Lens. London: Hazell, Watson, and Viney.
↑ Abney, W. de W. (1881). A Treatise on Photography (First ed.). London: Longmans, Green, and Co.
↑ Taylor, J. Traill (1892). The Optics of Photography and Photographic Lenses. London: Whittaker & Co.
↑ Hodges, John (1895). Photographic Lenses: How to Choose, and How to Use. Bradford: Percy Lund & Co.
↑ Derr, Louis (1906). Photography for students of physics and chemistry. London: Macmillan.
↑
↑ Johnson, George Lindsay (1909). Photographic Optics and Colour Photography. London: Ward & Co.

External links

http://www.dofmaster.com/dofjs.html to calculate hyperfocal distance and depth of field

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[Kingslake1951-1] 1 2 Kingslake, Rudolf (1951). Lenses in Photography: The Practical Guide to Optics for Photographers. Garden City, NY: Garden City Press.

[:0-2] 1 2 Sutton, Thomas; Dawson, George (1867). A Dictionary of Photography. London: Sampson Low, Son & Marston.

[3] Kingslake, Rudolf (1992). Optics in Photography - Google Books. ISBN 9780819407634 . Retrieved 24 September 2014.

[Piper1901-4] 1 2 Piper, C. Welborne (1901). A First Book of the Lens: An Elementary Treatise on the Action and Use of the Photographic Lens. London: Hazell, Watson, and Viney.

[5] Abney, W. de W. (1881). A Treatise on Photography (First ed.). London: Longmans, Green, and Co.

[6] Taylor, J. Traill (1892). The Optics of Photography and Photographic Lenses. London: Whittaker & Co.

[7] Hodges, John (1895). Photographic Lenses: How to Choose, and How to Use. Bradford: Percy Lund & Co.

[8] Derr, Louis (1906). Photography for students of physics and chemistry. London: Macmillan.

[9] ↑

[10] Johnson, George Lindsay (1909). Photographic Optics and Colour Photography. London: Ward & Co.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

v t e Photography
Equipment	Camera light-field digital field instant pinhole press rangefinder SLR still TLR toy view Darkroom enlarger safelight Drone Film base format holder stock available films discontinued films Filter Flash beauty dish cucoloris gobo hot shoe lens hood monolight reflector snoot softbox Lens prime zoom wide-angle fisheye telephoto Manufacturers Monopod Movie projector Slide projector Tripod head Zone plate
Terminology	35 mm equivalent focal length Angle of view Aperture Backscatter Black-and-white Chromatic aberration Circle of confusion Color balance Color temperature Depth of field Depth of focus Exposure Exposure compensation Exposure value Zebra patterning F-number Film format large medium Film speed Focal length Guide number Hyperfocal distance Lens flare Metering mode Perspective distortion Photograph Photographer Photographic printing Photographic processes Reciprocity Red-eye effect Science of photography Shutter speed Sync Zone System
Genres	Abstract Aerial Aircraft Architectural Astrophotography Banquet Candid Conceptual Conservation Cloudscape Documentary Ethnographic Erotic Fashion Fine-art Fire Forensic Glamour High-speed Landscape Nature Neues Sehen Nude Photojournalism Pictorialism Pornography Portrait Post-mortem Ruins Selfie Social documentary Sports Still life Stock Straight photography Street Toy camera Underwater Vernacular Wedding Wildlife
Techniques	Afocal Bokeh Brenizer Burst mode Contre-jour Cyanotype ETTR Fill flash Fireworks Harris shutter High-speed Holography Infrared Intentional camera movement Kirlian Kite aerial Long-exposure Luminogram Macro Mordançage Multiple exposure Multi-exposure HDR capture Night Panning Panoramic Photogram Print toning Redscale Rephotography Rollout Scanography Schlieren photography Sabattier effect Slow motion Stereoscopy Stopping down Strip Slit-scan Sun printing Tilt–shift Miniature faking Time-lapse Ultraviolet Vignetting Xerography Zoom burst
Composition	Diagonal method Framing Headroom Lead room Rule of thirds Simplicity Golden triangle (composition)
History	Timeline of photography technology Analog photography Autochrome Lumière Box camera Calotype Camera obscura Daguerreotype Dufaycolor Heliography Painted photography backdrops Photography and the law Glass plate Visual arts
Regional	Albania Bangladesh Canada China Denmark Greece India Japan Korea Luxembourg Norway Philippines Serbia Slovenia Sudan Taiwan Turkey Ukraine United States Uzbekistan Vietnam
Digital photography	Digital camera D-SLR comparison MILC camera back Digiscoping Comparison of digital and film photography Film scanner Image sensor CMOS APS CCD Three-CCD camera Foveon X3 sensor Image sharing Pixel
Color photography	Color Print film Chromogenic print Reversal film Color management color space primary color CMYK color model RGB color model
Photographic processing	Bleach bypass C-41 process Cross processing Developer Digital image processing Dye coupler E-6 process Fixer Gelatin silver process Gum printing Instant film K-14 process Print permanence Push processing Stop bath
Lists	Most expensive photographs Museums devoted to one photographer Photographs considered the most important Photographers Norwegian Polish street women
Related	Conservation and restoration of photographs film photographic plates Lomography Polaroid art Stereoscopy
Category Outline