Truncated 6-simplexes

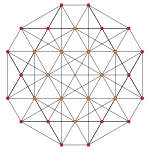
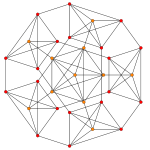
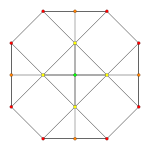
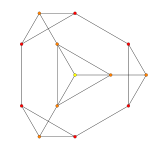
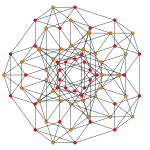
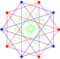
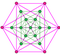
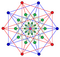
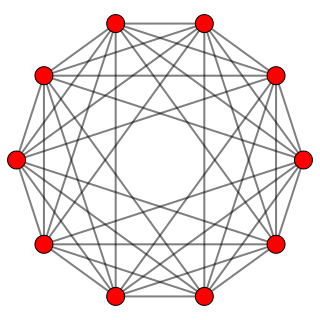
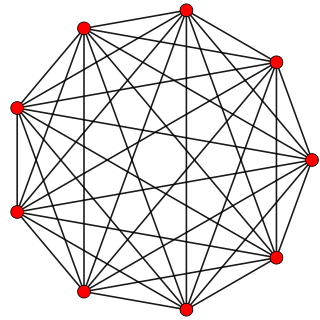
6-simplex	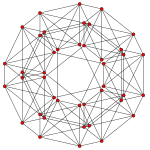Truncated 6-simplex
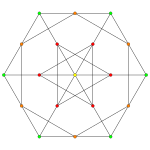
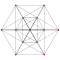
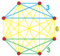
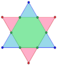
Bitruncated 6-simplex	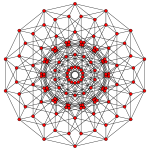Tritruncated 6-simplex
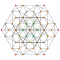
Orthogonal projections in A7 Coxeter plane

In six-dimensional geometry, a truncated 6-simplex is a convex uniform 6-polytope, being a truncation of the regular 6-simplex.

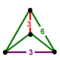
There are unique 3 degrees of truncation. Vertices of the truncation 6-simplex are located as pairs on the edge of the 6-simplex. Vertices of the bitruncated 6-simplex are located on the triangular faces of the 6-simplex. Vertices of the tritruncated 6-simplex are located inside the tetrahedral cells of the 6-simplex.

Truncated 6-simplex

Truncated 6-simplex
Type	uniform 6-polytope
Class	A6 polytope
Schläfli symbol	t{3,3,3,3,3}
Coxeter-Dynkin diagram
5-faces	14: 7 {3,3,3,3} 7 t{3,3,3,3}
4-faces	63: 42 {3,3,3} 21 t{3,3,3}
Cells	140: 105 {3,3} 35 t{3,3}
Faces	175: 140 {3} 35 {6}
Edges	126
Vertices	42
Vertex figure	( )v{3,3,3}
Coxeter group	A6, [35], order 5040
Dual	?
Properties	convex

Alternate names

• Truncated heptapeton (Acronym: til) (Jonathan Bowers) ^[1]

Coordinates

The vertices of the truncated 6-simplex can be most simply positioned in 7-space as permutations of (0,0,0,0,0,1,2). This construction is based on facets of the truncated 7-orthoplex.

Images

orthographic projections

Ak Coxeter plane	A6	A5	A4
Graph
Dihedral symmetry	[7]	[6]	[5]
Ak Coxeter plane	A3	A2
Graph
Dihedral symmetry	[4]	[3]

Bitruncated 6-simplex

Bitruncated 6-simplex
Type	uniform 6-polytope
Class	A6 polytope
Schläfli symbol	2t{3,3,3,3,3}
Coxeter-Dynkin diagram
5-faces	14
4-faces	84
Cells	245
Faces	385
Edges	315
Vertices	105
Vertex figure	{ }v{3,3}
Coxeter group	A6, [35], order 5040
Properties	convex

Alternate names

• Bitruncated heptapeton (Acronym: batal) (Jonathan Bowers) ^[2]

Coordinates

The vertices of the bitruncated 6-simplex can be most simply positioned in 7-space as permutations of (0,0,0,0,1,2,2). This construction is based on facets of the bitruncated 7-orthoplex.

Images

orthographic projections

Ak Coxeter plane	A6	A5	A4
Graph
Dihedral symmetry	[7]	[6]	[5]
Ak Coxeter plane	A3	A2
Graph
Dihedral symmetry	[4]	[3]

Tritruncated 6-simplex

Tritruncated 6-simplex
Type	uniform 6-polytope
Class	A6 polytope
Schläfli symbol	3t{3,3,3,3,3}
Coxeter-Dynkin diagram	or
5-faces	14 2t{3,3,3,3}
4-faces	84
Cells	280
Faces	490
Edges	420
Vertices	140
Vertex figure	{3}v{3}
Coxeter group	A6, [[35]], order 10080
Properties	convex, isotopic

The tritruncated 6-simplex is an isotopic uniform polytope, with 14 identical bitruncated 5-simplex facets.

The tritruncated 6-simplex is the intersection of two 6-simplexes in dual configuration: and .

Alternate names

• Tetradecapeton (as a 14-facetted 6-polytope) (Acronym: fe) (Jonathan Bowers) ^[3]

Coordinates

The vertices of the tritruncated 6-simplex can be most simply positioned in 7-space as permutations of (0,0,0,1,2,2,2). This construction is based on facets of the bitruncated 7-orthoplex. Alternately it can be centered on the origin as permutations of (-1,-1,-1,0,1,1,1).

Images

orthographic projections

Ak Coxeter plane	A6	A5	A4
Graph
Symmetry	[[7]](*)=[14]	[6]	[[5]](*)=[10]
Ak Coxeter plane	A3	A2
Graph
Symmetry	[4]	[[3]](*)=[6]

Note: (*) Symmetry doubled for A_k graphs with even k due to symmetrically-ringed Coxeter-Dynkin diagram.

Related polytopes

Isotopic uniform truncated simplices

Dim.	2	3	4	5	6	7	8
Name Coxeter	Hexagon = t{3} = {6}	Octahedron = r{3,3} = {31,1} = {3,4} ${\displaystyle \left\{{\begin{array}{l}3\\3\end{array}}\right\}}$	Decachoron 2t{33}	Dodecateron 2r{34} = {32,2} ${\displaystyle \left\{{\begin{array}{l}3,3\\3,3\end{array}}\right\}}$	Tetradecapeton 3t{35}	Hexadecaexon 3r{36} = {33,3} ${\displaystyle \left\{{\begin{array}{l}3,3,3\\3,3,3\end{array}}\right\}}$	Octadecazetton 4t{37}
Images
Vertex figure	( )∨( )	{ }×{ }	{ }∨{ }	{3}×{3}	{3}∨{3}	{3,3}×{3,3}	{3,3}∨{3,3}
Facets		{3}	t{3,3}	r{3,3,3}	2t{3,3,3,3}	2r{3,3,3,3,3}	3t{3,3,3,3,3,3}
As intersecting dual simplexes	∩	∩	∩	∩	∩	∩	∩

Related uniform 6-polytopes

The truncated 6-simplex is one of 35 uniform 6-polytopes based on the [3,3,3,3,3] Coxeter group, all shown here in A₆ Coxeter plane orthographic projections.

A6 polytopes
t0	t1	t2	t0,1	t0,2	t1,2	t0,3	t1,3	t2,3
t0,4	t1,4	t0,5	t0,1,2	t0,1,3	t0,2,3	t1,2,3	t0,1,4	t0,2,4
t1,2,4	t0,3,4	t0,1,5	t0,2,5	t0,1,2,3	t0,1,2,4	t0,1,3,4	t0,2,3,4	t1,2,3,4
t0,1,2,5	t0,1,3,5	t0,2,3,5	t0,1,4,5	t0,1,2,3,4	t0,1,2,3,5	t0,1,2,4,5	t0,1,2,3,4,5

Notes

1. Klitzing, (o3x3o3o3o3o - til).
2. Klitzing, (o3x3x3o3o3o - batal).
3. Klitzing, (o3o3x3x3o3o - fe).

References

• H.S.M. Coxeter:
  • H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
  • Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, wiley.com, ISBN   978-0-471-01003-6
    • (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
    • (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
    • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
• Norman Johnson Uniform Polytopes, Manuscript (1991)
  • N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D.
• Klitzing, Richard. "6D uniform polytopes (polypeta) with acronyms". o3x3o3o3o3o - til, o3x3x3o3o3o - batal, o3o3x3x3o3o - fe

External links

• Polytopes of Various Dimensions
• Multi-dimensional Glossary

v t e Fundamental convex regular and uniform polytopes in dimensions 2–10
Family	An	Bn	I2(p) / Dn	E6 / E7 / E8 / F4 / G2	Hn
Regular polygon	Triangle	Square	p-gon	Hexagon	Pentagon
Uniform polyhedron	Tetrahedron	Octahedron • Cube	Demicube		Dodecahedron • Icosahedron
Uniform polychoron	Pentachoron	16-cell • Tesseract	Demitesseract	24-cell	120-cell • 600-cell
Uniform 5-polytope	5-simplex	5-orthoplex • 5-cube	5-demicube
Uniform 6-polytope	6-simplex	6-orthoplex • 6-cube	6-demicube	122 • 221
Uniform 7-polytope	7-simplex	7-orthoplex • 7-cube	7-demicube	132 • 231 • 321
Uniform 8-polytope	8-simplex	8-orthoplex • 8-cube	8-demicube	142 • 241 • 421
Uniform 9-polytope	9-simplex	9-orthoplex • 9-cube	9-demicube
Uniform 10-polytope	10-simplex	10-orthoplex • 10-cube	10-demicube
Uniform n-polytope	n-simplex	n-orthoplex • n-cube	n-demicube	1k2 • 2k1 • k21	n-pentagonal polytope
Topics: Polytope families • Regular polytope • List of regular polytopes and compounds