An evolutionarily stable strategy (ESS) is a strategy that is impermeable when adopted by a population in adaptation to a specific environment, that is to say it cannot be displaced by an alternative strategy which may be novel or initially rare. Introduced by John Maynard Smith and George R. Price in 1972/3, it is an important concept in behavioural ecology, evolutionary psychology, mathematical game theory and economics, with applications in other fields such as anthropology, philosophy and political science.

John Maynard Smith was a British theoretical and mathematical evolutionary biologist and geneticist. Originally an aeronautical engineer during the Second World War, he took a second degree in genetics under the well-known biologist J. B. S. Haldane. Maynard Smith was instrumental in the application of game theory to evolution with George R. Price, and theorised on other problems such as the evolution of sex and signalling theory.

Sexual selection is a mode of natural selection in which members of one biological sex choose mates of the other sex to mate with, and compete with members of the same sex for access to members of the opposite sex. These two forms of selection mean that some individuals have greater reproductive success than others within a population, for example because they are more attractive or prefer more attractive partners to produce offspring. Successful males benefit from frequent mating and monopolizing access to one or more fertile females. Females can maximise the return on the energy they invest in reproduction by selecting and mating with the best males.
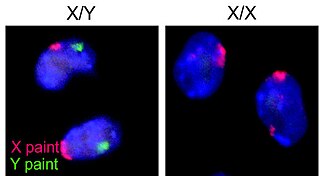
Sex is the trait that determines whether a sexually reproducing organism produces male or female gametes. Male plants and animals produce small mobile gametes, while females produce larger, non-motile ones. Organisms that produce both types of gametes are called hermaphrodites. During sexual reproduction, male and female gametes fuse to form zygotes, which develop into offspring that inherit traits from each parent.

William Donald Hamilton was a British evolutionary biologist, recognised as one of the most significant evolutionary theorists of the 20th century.

Fitness is the quantitative representation of individual reproductive success. It is also equal to the average contribution to the gene pool of the next generation, made by the same individuals of the specified genotype or phenotype. Fitness can be defined either with respect to a genotype or to a phenotype in a given environment or time. The fitness of a genotype is manifested through its phenotype, which is also affected by the developmental environment. The fitness of a given phenotype can also be different in different selective environments.
A sex ratio is the ratio of males to females in a population. As explained by Fisher's principle, for evolutionary reasons this is typically about 1:1 in species which reproduce sexually. However, many species deviate from an even sex ratio, either periodically or permanently. Examples include parthenogenic species, periodically mating organisms such as aphids, some eusocial wasps, bees, ants, and termites.

George Robert Price was an American population geneticist. Price is often noted for his formulation of the Price equation in 1967.
Evolutionary game theory (EGT) is the application of game theory to evolving populations in biology. It defines a framework of contests, strategies, and analytics into which Darwinian competition can be modelled. It originated in 1973 with John Maynard Smith and George R. Price's formalisation of contests, analysed as strategies, and the mathematical criteria that can be used to predict the results of competing strategies.
Linear discriminant analysis (LDA), normal discriminant analysis (NDA), or discriminant function analysis is a generalization of Fisher's linear discriminant, a method used in statistics and other fields, to find a linear combination of features that characterizes or separates two or more classes of objects or events. The resulting combination may be used as a linear classifier, or, more commonly, for dimensionality reduction before later classification.
The drawdown is the measure of the decline from a historical peak in some variable.

The secretary problem demonstrates a scenario involving optimal stopping theory that is studied extensively in the fields of applied probability, statistics, and decision theory. It is also known as the marriage problem, the sultan's dowry problem, the fussy suitor problem, the googol game, and the best choice problem.
A population can be described as being in an evolutionarily stable state when that population's "genetic composition is restored by selection after a disturbance, provided the disturbance is not too large". This population as a whole can be either monomorphic or polymorphic. This is now referred to as convergent stability.
Sex allocation is the allocation of resources to male versus female reproduction in sexual species. Sex allocation theory tries to explain why many species produce equal number of males and females.
Fisher's principle is an evolutionary model that explains why the sex ratio of most species that produce offspring through sexual reproduction is approximately 1:1 between males and females. A. W. F. Edwards has remarked that it is "probably the most celebrated argument in evolutionary biology".
Sex-limited genes are genes that are present in both sexes of sexually reproducing species but are expressed in only one sex and have no penetrance, or are simply 'turned off' in the other. In other words, sex-limited genes cause the two sexes to show different traits or phenotypes, despite having the same genotype. This term is restricted to autosomal traits, and should not be confused with sex-linked characteristics, which have to do with genetic differences on the sex chromosomes. Sex-limited genes are also distinguished from sex-influenced genes, where the same gene will show differential expression in each sex. Sex-influenced genes commonly show a dominant/recessive relationship, where the same gene will have a dominant effect in one sex and a recessive effect in the other. However, the resulting phenotypes caused by sex-limited genes are present in only one sex and can be seen prominently in various species that typically show high sexual dimorphism.
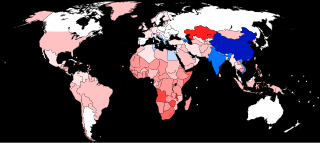
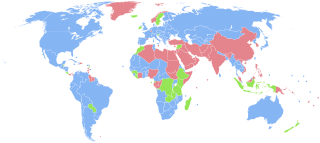
The human sex ratio is the ratio of males to females in a population in the context of anthropology and demography. In humans, the natural sex ratio at birth is slightly biased towards the male sex. It is estimated to be about 1.05 or 1.06 or within a narrow range from 1.03 to 1.06 males per female.

In the study of graph coloring problems in mathematics and computer science, a greedy coloring or sequential coloring is a coloring of the vertices of a graph formed by a greedy algorithm that considers the vertices of the graph in sequence and assigns each vertex its first available color. Greedy colorings can be found in linear time, but they do not, in general, use the minimum number of colors possible.
Mean-field game theory is the study of strategic decision making by small interacting agents in very large populations. It lies at the intersection of game theory with stochastic analysis and control theory. The use of the term "mean field" is inspired by mean-field theory in physics, which considers the behavior of systems of large numbers of particles where individual particles have negligible impacts upon the system. In other words, each agent acts according to his minimization or maximization problem taking into account other agents’ decisions and because their population is large we can assume the number of agents goes to infinity and a representative agent exists.
In computer science, an optimal binary search tree (Optimal BST), sometimes called a weight-balanced binary tree, is a binary search tree which provides the smallest possible search time (or expected search time) for a given sequence of accesses (or access probabilities). Optimal BSTs are generally divided into two types: static and dynamic.















