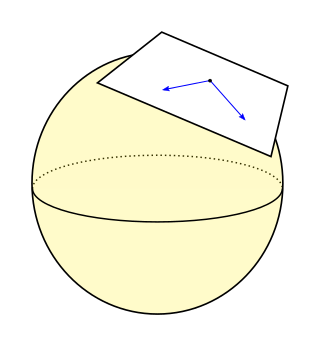
In differential geometry, a Riemannian manifold is a geometric space on which many geometric notions such as distance, angles, length, volume, and curvature are defined. Euclidean space, the -sphere, hyperbolic space, and smooth surfaces in three-dimensional space, such as ellipsoids and paraboloids, are all examples of Riemannian manifolds. Riemannian manifolds are named after German mathematician Bernhard Riemann, who first conceptualized them.

In mathematics, Thurston's geometrization conjecture states that each of certain three-dimensional topological spaces has a unique geometric structure that can be associated with it. It is an analogue of the uniformization theorem for two-dimensional surfaces, which states that every simply connected Riemann surface can be given one of three geometries.

In the mathematical disciplines of topology and geometry, an orbifold is a generalization of a manifold. Roughly speaking, an orbifold is a topological space that is locally a finite group quotient of a Euclidean space.
In mathematics, a generalized flag variety is a homogeneous space whose points are flags in a finite-dimensional vector space V over a field F. When F is the real or complex numbers, a generalized flag variety is a smooth or complex manifold, called a real or complexflag manifold. Flag varieties are naturally projective varieties.
This is a glossary of some terms used in Riemannian geometry and metric geometry — it doesn't cover the terminology of differential topology.
In mathematics, an automorphic function is a function on a space that is invariant under the action of some group, in other words a function on the quotient space. Often the space is a complex manifold and the group is a discrete group.

In mathematics, a symmetric space is a Riemannian manifold whose group of isometries contains an inversion symmetry about every point. This can be studied with the tools of Riemannian geometry, leading to consequences in the theory of holonomy; or algebraically through Lie theory, which allowed Cartan to give a complete classification. Symmetric spaces commonly occur in differential geometry, representation theory and harmonic analysis.
In mathematics, more particularly in the fields of dynamical systems and geometric topology, an Anosov map on a manifold M is a certain type of mapping, from M to itself, with rather clearly marked local directions of "expansion" and "contraction". Anosov systems are a special case of Axiom A systems.

In mathematics, a Hermitian symmetric space is a Hermitian manifold which at every point has an inversion symmetry preserving the Hermitian structure. First studied by Élie Cartan, they form a natural generalization of the notion of Riemannian symmetric space from real manifolds to complex manifolds.
In mathematics, a solvmanifold is a homogeneous space of a connected solvable Lie group. It may also be characterized as a quotient of a connected solvable Lie group by a closed subgroup. A special class of solvmanifolds, nilmanifolds, was introduced by Anatoly Maltsev, who proved the first structural theorems. Properties of general solvmanifolds are similar, but somewhat more complicated.
In mathematics, the Abel–Jacobi map is a construction of algebraic geometry which relates an algebraic curve to its Jacobian variety. In Riemannian geometry, it is a more general construction mapping a manifold to its Jacobi torus. The name derives from the theorem of Abel and Jacobi that two effective divisors are linearly equivalent if and only if they are indistinguishable under the Abel–Jacobi map.

In Lie theory and related areas of mathematics, a lattice in a locally compact group is a discrete subgroup with the property that the quotient space has finite invariant measure. In the special case of subgroups of Rn, this amounts to the usual geometric notion of a lattice as a periodic subset of points, and both the algebraic structure of lattices and the geometry of the space of all lattices are relatively well understood.
In geometry, if X is a manifold with an action of a topological group G by analytical diffeomorphisms, the notion of a (G, X)-structure on a topological space is a way to formalise it being locally isomorphic to X with its G-invariant structure; spaces with a (G, X)-structure are always manifolds and are called (G, X)-manifolds. This notion is often used with G being a Lie group and X a homogeneous space for G. Foundational examples are hyperbolic manifolds and affine manifolds.

In the theory of Lie groups, the exponential map is a map from the Lie algebra of a Lie group to the group, which allows one to recapture the local group structure from the Lie algebra. The existence of the exponential map is one of the primary reasons that Lie algebras are a useful tool for studying Lie groups.
Local rigidity theorems in the theory of discrete subgroups of Lie groups are results which show that small deformations of certain such subgroups are always trivial. It is different from Mostow rigidity and weaker than superrigidity.
Arithmetic Fuchsian groups are a special class of Fuchsian groups constructed using orders in quaternion algebras. They are particular instances of arithmetic groups. The prototypical example of an arithmetic Fuchsian group is the modular group . They, and the hyperbolic surface associated to their action on the hyperbolic plane often exhibit particularly regular behaviour among Fuchsian groups and hyperbolic surfaces.
In Lie theory, an area of mathematics, the Kazhdan–Margulis theorem is a statement asserting that a discrete subgroup in semisimple Lie groups cannot be too dense in the group. More precisely, in any such Lie group there is a uniform neighbourhood of the identity element such that every lattice in the group has a conjugate whose intersection with this neighbourhood contains only the identity. This result was proven in the 1960s by David Kazhdan and Grigory Margulis.
In the mathematical subject of geometric group theory, the Švarc–Milnor lemma is a statement which says that a group , equipped with a "nice" discrete isometric action on a metric space , is quasi-isometric to .
In the mathematical subject of group theory, a co-Hopfian group is a group that is not isomorphic to any of its proper subgroups. The notion is dual to that of a Hopfian group, named after Heinz Hopf.
In differential geometry, Mal'cev's criterion, proved by Anatoly Mal'cev, states that a simply connected nilpotent Lie group admits a lattice, i.e., a discrete co-compact subgroup, if and only if the associated Lie algebra admits a basis such that the structure constants are rational.





















