This is a list of particular manifolds, by Wikipedia page. See also list of geometric topology topics. For categorical listings see Category:Manifolds and its subcategories.
Lie groups provide several interesting families. See Table of Lie groups for examples. See also: List of simple Lie groups and List of Lie group topics.
For more examples see 3-manifold.
For more examples see 4-manifold.

In mathematics, differential topology is the field dealing with the topological properties and smooth properties of smooth manifolds. In this sense differential topology is distinct from the closely related field of differential geometry, which concerns the geometric properties of smooth manifolds, including notions of size, distance, and rigid shape. By comparison differential topology is concerned with coarser properties, such as the number of holes in a manifold, its homotopy type, or the structure of its diffeomorphism group. Because many of these coarser properties may be captured algebraically, differential topology has strong links to algebraic topology.

Differential geometry is a mathematical discipline that studies the geometry of smooth shapes and smooth spaces, otherwise known as smooth manifolds. It uses the techniques of differential calculus, integral calculus, linear algebra and multilinear algebra. The field has its origins in the study of spherical geometry as far back as antiquity. It also relates to astronomy, the geodesy of the Earth, and later the study of hyperbolic geometry by Lobachevsky. The simplest examples of smooth spaces are the plane and space curves and surfaces in the three-dimensional Euclidean space, and the study of these shapes formed the basis for development of modern differential geometry during the 18th and 19th centuries.
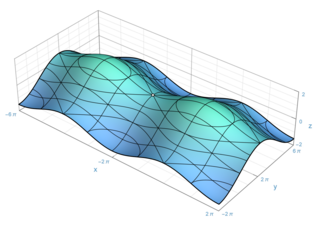
In the part of mathematics referred to as topology, a surface is a two-dimensional manifold. Some surfaces arise as the boundaries of three-dimensional solids; for example, the sphere is the boundary of the solid ball. Other surfaces arise as graphs of functions of two variables; see the figure at right. However, surfaces can also be defined abstractly, without reference to any ambient space. For example, the Klein bottle is a surface that cannot be embedded in three-dimensional Euclidean space.

Symplectic geometry is a branch of differential geometry and differential topology that studies symplectic manifolds; that is, differentiable manifolds equipped with a closed, nondegenerate 2-form. Symplectic geometry was founded by the Russian mathematician Vladimir Arnold and has its origins in the Hamiltonian formulation of classical mechanics where the phase space of certain classical systems takes on the structure of a symplectic manifold.
In mathematics and especially differential geometry, a Kähler manifold is a manifold with three mutually compatible structures: a complex structure, a Riemannian structure, and a symplectic structure. The concept was first studied by Jan Arnoldus Schouten and David van Dantzig in 1930, and then introduced by Erich Kähler in 1933. The terminology has been fixed by André Weil. Kähler geometry refers to the study of Kähler manifolds, their geometry and topology, as well as the study of structures and constructions that can be performed on Kähler manifolds, such as the existence of special connections like Hermitian Yang–Mills connections, or special metrics such as Kähler–Einstein metrics.

In differential geometry and complex geometry, a complex manifold is a manifold with an atlas of charts to the open unit disc in , such that the transition maps are holomorphic.

In mathematics, low-dimensional topology is the branch of topology that studies manifolds, or more generally topological spaces, of four or fewer dimensions. Representative topics are the structure theory of 3-manifolds and 4-manifolds, knot theory, and braid groups. This can be regarded as a part of geometric topology. It may also be used to refer to the study of topological spaces of dimension 1, though this is more typically considered part of continuum theory.
In the mathematical field of differential geometry, Ricci-flatness is a condition on the curvature of a (pseudo-)Riemannian manifold. Ricci-flat manifolds are a special kind of Einstein manifold. In theoretical physics, Ricci-flat Lorentzian manifolds are of fundamental interest, as they are the solutions of Einstein's field equations in vacuum with vanishing cosmological constant.
In differential geometry, a hyperkähler manifold is a Riemannian manifold of dimension and holonomy group contained in Sp(k). Hyperkähler manifolds are special classes of Kähler manifolds. They can be thought of as quaternionic analogues of Kähler manifolds. All hyperkähler manifolds are Ricci-flat and are thus Calabi–Yau manifolds.

In mathematics, a 3-manifold is a space that locally looks like Euclidean 3-dimensional space. A 3-manifold can be thought of as a possible shape of the universe. Just as a sphere looks like a plane to a small enough observer, all 3-manifolds look like our universe does to a small enough observer. This is made more precise in the definition below.
In mathematics, a manifold is a topological space that locally resembles Euclidean space near each point. More precisely, an n-dimensional manifold, or n-manifold for short, is a topological space with the property that each point has a neighborhood that is homeomorphic to an open subset of n-dimensional Euclidean space.
In differential geometry, a quaternion-Kähler manifold is a Riemannian 4n-manifold whose Riemannian holonomy group is a subgroup of Sp(n)·Sp(1) for some . Here Sp(n) is the sub-group of consisting of those orthogonal transformations that arise by left-multiplication by some quaternionic matrix, while the group of unit-length quaternions instead acts on quaternionic -space by right scalar multiplication. The Lie group generated by combining these actions is then abstractly isomorphic to .
In mathematics, a nilmanifold is a differentiable manifold which has a transitive nilpotent group of diffeomorphisms acting on it. As such, a nilmanifold is an example of a homogeneous space and is diffeomorphic to the quotient space , the quotient of a nilpotent Lie group N modulo a closed subgroup H. This notion was introduced by Anatoly Mal'cev in 1951.
In differential geometry, a hypercomplex manifold is a manifold with the tangent bundle equipped with an action by the algebra of quaternions in such a way that the quaternions define integrable almost complex structures.
In topology, a branch of mathematics, an aspherical space is a topological space with all homotopy groups equal to 0 when .
In mathematics, specifically geometry and topology, the classification of manifolds is a basic question, about which much is known, and many open questions remain.
The Geometry Festival is an annual mathematics conference held in the United States.
Mathematics is a broad subject that is commonly divided in many areas that may be defined by their objects of study, by the used methods, or by both. For example, analytic number theory is a subarea of number theory devoted to the use of methods of analysis for the study of natural numbers.