
In mathematics, the gamma function is one commonly used extension of the factorial function to complex numbers. The gamma function is defined for all complex numbers except the non-positive integers. For every positive integer n,

In geometry, a tetrahedron, also known as a triangular pyramid, is a polyhedron composed of four triangular faces, six straight edges, and four vertices. The tetrahedron is the simplest of all the ordinary convex polyhedra.

In trigonometry, the law of sines, sine law, sine formula, or sine rule is an equation relating the lengths of the sides of any triangle to the sines of its angles. According to the law,

In geometry, the incircle or inscribed circle of a triangle is the largest circle that can be contained in the triangle; it touches the three sides. The center of the incircle is a triangle center called the triangle's incenter.
In mechanics and geometry, the 3D rotation group, often denoted O(3), is the group of all rotations about the origin of three-dimensional Euclidean space under the operation of composition.

In Euclidean geometry, a cyclic quadrilateral or inscribed quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic. The center of the circle and its radius are called the circumcenter and the circumradius respectively. Other names for these quadrilaterals are concyclic quadrilateral and chordal quadrilateral, the latter since the sides of the quadrilateral are chords of the circumcircle. Usually the quadrilateral is assumed to be convex, but there are also crossed cyclic quadrilaterals. The formulas and properties given below are valid in the convex case.

In mathematics, the digamma function is defined as the logarithmic derivative of the gamma function:

In mathematics, theta functions are special functions of several complex variables. They show up in many topics, including Abelian varieties, moduli spaces, quadratic forms, and solitons. As Grassmann algebras, they appear in quantum field theory.
In mathematics, the Jacobi elliptic functions are a set of basic elliptic functions. They are found in the description of the motion of a pendulum, as well as in the design of electronic elliptic filters. While trigonometric functions are defined with reference to a circle, the Jacobi elliptic functions are a generalization which refer to other conic sections, the ellipse in particular. The relation to trigonometric functions is contained in the notation, for example, by the matching notation for . The Jacobi elliptic functions are used more often in practical problems than the Weierstrass elliptic functions as they do not require notions of complex analysis to be defined and/or understood. They were introduced by Carl Gustav Jakob Jacobi. Carl Friedrich Gauss had already studied special Jacobi elliptic functions in 1797, the lemniscate elliptic functions in particular, but his work was published much later.
In geometry, the circumscribed circle or circumcircle of a triangle is a circle that passes through all three vertices. The center of this circle is called the circumcenter of the triangle, and its radius is called the circumradius. The circumcenter is the point of intersection between the three perpendicular bisectors of the triangle's sides, and is a triangle center.
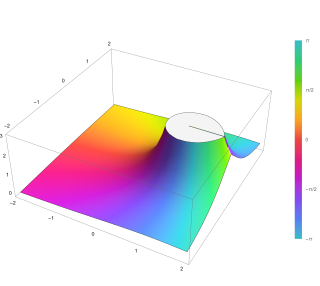
In mathematics, the Gaussian or ordinary hypergeometric function2F1(a,b;c;z) is a special function represented by the hypergeometric series, that includes many other special functions as specific or limiting cases. It is a solution of a second-order linear ordinary differential equation (ODE). Every second-order linear ODE with three regular singular points can be transformed into this equation.

In mathematics, the lemniscate constantϖ is a transcendental mathematical constant that is the ratio of the perimeter of Bernoulli's lemniscate to its diameter, analogous to the definition of π for the circle. Equivalently, the perimeter of the lemniscate is 2ϖ. The lemniscate constant is closely related to the lemniscate elliptic functions and approximately equal to 2.62205755. The symbol ϖ is a cursive variant of π; see Pi § Variant pi.

In geometry, Bretschneider's formula is a mathematical expression for the area of a general quadrilateral. It works on both convex and concave quadrilaterals, whether it is cyclic or not.
In geometry, calculating the area of a triangle is an elementary problem encountered often in many different situations. The best known and simplest formula is where b is the length of the base of the triangle, and h is the height or altitude of the triangle. The term "base" denotes any side, and "height" denotes the length of a perpendicular from the vertex opposite the base onto the line containing the base. Euclid proved that the area of a triangle is half that of a parallelogram with the same base and height in his book Elements in 300 BCE. In 499 CE Aryabhata, used this illustrated method in the Aryabhatiya.
In hyperbolic geometry, the "law of cosines" is a pair of theorems relating the sides and angles of triangles on a hyperbolic plane, analogous to the planar law of cosines from plane trigonometry, or the spherical law of cosines in spherical trigonometry. It can also be related to the relativistic velocity addition formula.

In geometry, a ball is a region in a space comprising all points within a fixed distance, called the radius, from a given point; that is, it is the region enclosed by a sphere or hypersphere. An n-ball is a ball in an n-dimensional Euclidean space. The volume of a n-ball is the Lebesgue measure of this ball, which generalizes to any dimension the usual volume of a ball in 3-dimensional space. The volume of a n-ball of radius R is where is the volume of the unit n-ball, the n-ball of radius 1.

In trigonometry, Mollweide's formula is a pair of relationships between sides and angles in a triangle.
Solution of triangles is the main trigonometric problem of finding the characteristics of a triangle, when some of these are known. The triangle can be located on a plane or on a sphere. Applications requiring triangle solutions include geodesy, astronomy, construction, and navigation.

In trigonometry, the law of cotangents is a relationship among the lengths of the sides of a triangle and the cotangents of the halves of the three angles.



































































































