An adjective is a word that describes or defines a noun or noun phrase. Its semantic role is to change information given by the noun.

In probability theory and statistics, the gamma distribution is a versatile two-parameter family of continuous probability distributions. The exponential distribution, Erlang distribution, and chi-squared distribution are special cases of the gamma distribution. There are two equivalent parameterizations in common use:
- With a shape parameter k and a scale parameter θ
- With a shape parameter and an inverse scale parameter , called a rate parameter.
In linguistics, a modifier is an optional element in phrase structure or clause structure which modifies the meaning of another element in the structure. For instance, the adjective "red" acts as a modifier in the noun phrase "red ball", providing extra details about which particular ball is being referred to. Similarly, the adverb "quickly" acts as a modifier in the verb phrase "run quickly". Modification can be considered a high-level domain of the functions of language, on par with predication and reference.
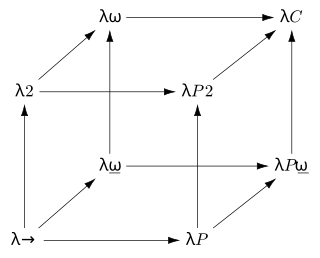
In mathematical logic and type theory, the λ-cube is a framework introduced by Henk Barendregt to investigate the different dimensions in which the calculus of constructions is a generalization of the simply typed λ-calculus. Each dimension of the cube corresponds to a new kind of dependency between terms and types. Here, "dependency" refers to the capacity of a term or type to bind a term or type. The respective dimensions of the λ-cube correspond to:

In probability theory and statistics, the inverse gamma distribution is a two-parameter family of continuous probability distributions on the positive real line, which is the distribution of the reciprocal of a variable distributed according to the gamma distribution.

In probability and statistics, the Kumaraswamy's double bounded distribution is a family of continuous probability distributions defined on the interval (0,1). It is similar to the beta distribution, but much simpler to use especially in simulation studies since its probability density function, cumulative distribution function and quantile functions can be expressed in closed form. This distribution was originally proposed by Poondi Kumaraswamy for variables that are lower and upper bounded with a zero-inflation. This was extended to inflations at both extremes [0,1] in later work with S. G. Fletcher.

The Duffing equation, named after Georg Duffing (1861–1944), is a non-linear second-order differential equation used to model certain damped and driven oscillators. The equation is given by where the (unknown) function is the displacement at time t, is the first derivative of with respect to time, i.e. velocity, and is the second time-derivative of i.e. acceleration. The numbers and are given constants.

In directional statistics, the Kent distribution, also known as the 5-parameter Fisher–Bingham distribution, is a probability distribution on the unit sphere. It is the analogue on S2 of the bivariate normal distribution with an unconstrained covariance matrix. The Kent distribution was proposed by John T. Kent in 1982, and is used in geology as well as bioinformatics.
The normal-inverse Gaussian distribution is a continuous probability distribution that is defined as the normal variance-mean mixture where the mixing density is the inverse Gaussian distribution. The NIG distribution was noted by Blaesild in 1977 as a subclass of the generalised hyperbolic distribution discovered by Ole Barndorff-Nielsen. In the next year Barndorff-Nielsen published the NIG in another paper. It was introduced in the mathematical finance literature in 1997.

A biarc is a smooth curve formed from two circular arcs. In order to make the biarc smooth, the two arcs should have the same tangent at the connecting point where they meet.
In mathematics, the Veblen functions are a hierarchy of normal functions, introduced by Oswald Veblen in Veblen (1908). If φ0 is any normal function, then for any non-zero ordinal α, φα is the function enumerating the common fixed points of φβ for β<α. These functions are all normal.

In probability theory and statistics, the normal-inverse-gamma distribution is a four-parameter family of multivariate continuous probability distributions. It is the conjugate prior of a normal distribution with unknown mean and variance.
A synchronous frame is a reference frame in which the time coordinate defines proper time for all co-moving observers. It is built by choosing some constant time hypersurface as an origin, such that has in every point a normal along the time line and a light cone with an apex in that point can be constructed; all interval elements on this hypersurface are space-like. A family of geodesics normal to this hypersurface are drawn and defined as the time coordinates with a beginning at the hypersurface. In terms of metric-tensor components , a synchronous frame is defined such that
Head grammar (HG) is a grammar formalism introduced in Carl Pollard (1984) as an extension of the context-free grammar class of grammars. Head grammar is therefore a type of phrase structure grammar, as opposed to a dependency grammar. The class of head grammars is a subset of the linear context-free rewriting systems.
In probability theory, a beta negative binomial distribution is the probability distribution of a discrete random variable equal to the number of failures needed to get successes in a sequence of independent Bernoulli trials. The probability of success on each trial stays constant within any given experiment but varies across different experiments following a beta distribution. Thus the distribution is a compound probability distribution.
In mathematics, Ricci calculus constitutes the rules of index notation and manipulation for tensors and tensor fields on a differentiable manifold, with or without a metric tensor or connection. It is also the modern name for what used to be called the absolute differential calculus, developed by Gregorio Ricci-Curbastro in 1887–1896, and subsequently popularized in a paper written with his pupil Tullio Levi-Civita in 1900. Jan Arnoldus Schouten developed the modern notation and formalism for this mathematical framework, and made contributions to the theory, during its applications to general relativity and differential geometry in the early twentieth century.
In linguistics, a subsective modifier is an expression which modifies another by delivering a subset of its denotation. For instance, the English adjective "skilled" is subsective since being a skilled surgeon entails being a surgeon. By contrast, the English adjective "alleged" is non-subsective since an "alleged spy" need not be an actual spy.
In linguistics, a privative adjective is an adjective which seems to exclude members of the extension of the noun which it modifies. For instance, "fake" is privative since a "fake nose" is not an actual nose. Other examples in English include "pretend", "fictitious", and "artificial". The defining feature of privative adjectives is shown below in set theoretic notation.
- An adjective is privative if for any noun , we have that .
In probability theory and statistics, the modified half-normal distribution (MHN) is a three-parameter family of continuous probability distributions supported on the positive part of the real line. It can be viewed as a generalization of multiple families, including the half-normal distribution, truncated normal distribution, gamma distribution, and square root of the gamma distribution, all of which are special cases of the MHN distribution. Therefore, it is a flexible probability model for analyzing real-valued positive data. The name of the distribution is motivated by the similarities of its density function with that of the half-normal distribution.
In mathematics, Rathjen's psi function is an ordinal collapsing function developed by Michael Rathjen. It collapses weakly Mahlo cardinals to generate large countable ordinals. A weakly Mahlo cardinal is a cardinal such that the set of regular cardinals below is closed under . Rathjen uses this to diagonalise over the weakly inaccessible hierarchy.














