Celestial coordinate system

Last updated July 10, 2021

In astronomy, a celestial coordinate system (or celestial reference system) is a system for specifying positions of satellites, planets, stars, galaxies, and other celestial objects relative to physical reference points available to a situated observer (e.g. the true horizon and north cardinal direction to an observer situated on the Earth's surface).^[1] Coordinate systems can specify an object's position in three-dimensional space or plot merely its direction on a celestial sphere, if the object's distance is unknown or trivial.

The coordinate systems are implemented in either spherical or rectangular coordinates. Spherical coordinates, projected on the celestial sphere, are analogous to the geographic coordinate system used on the surface of Earth. These differ in their choice of fundamental plane, which divides the celestial sphere into two equal hemispheres along a great circle. Rectangular coordinates, in appropriate units, are simply the Cartesian equivalent of the spherical coordinates, with the same fundamental ( $x, y$ ) plane and primary ( $x$ -axis) direction. Each coordinate system is named after its choice of fundamental plane.

Coordinate systems

The following table lists the common coordinate systems in use by the astronomical community. The fundamental plane divides the celestial sphere into two equal hemispheres and defines the baseline for the latitudinal coordinates, similar to the equator in the geographic coordinate system. The poles are located at ±90° from the fundamental plane. The primary direction is the starting point of the longitudinal coordinates. The origin is the zero distance point, the "center of the celestial sphere", although the definition of celestial sphere is ambiguous about the definition of its center point.

Coordinate system^[2]	Center point (origin)	Fundamental plane (0° latitude)	Poles	Coordinates		Primary direction (0° longitude)
Coordinate system^[2]	Center point (origin)	Fundamental plane (0° latitude)	Poles	Latitude	Longitude	Primary direction (0° longitude)
Horizontal (also called alt-az or el-az)	Observer	Horizon	Zenith, nadir	Altitude ( $a$ ) or elevation	Azimuth ( $A$ )	North or south point of horizon
Equatorial	Center of the Earth (geocentric), or Sun (heliocentric)	Celestial equator	Celestial poles	Declination ( $δ$ )	Right ascension ( $α$ ) or hour angle ( $h$ )	March equinox
Ecliptic	Center of the Earth (geocentric), or Sun (heliocentric)	Ecliptic	Ecliptic poles	Ecliptic latitude ( $β$ )	Ecliptic longitude ( $λ$ )	March equinox
Galactic	Center of the Sun	Galactic plane	Galactic poles	Galactic latitude ( $b$ )	Galactic longitude ( $l$ )	Galactic Center
Supergalactic		Supergalactic plane	Supergalactic poles	Supergalactic latitude ( $SGB$ )	Supergalactic longitude ( $SGL$ )	Intersection of supergalactic plane and galactic plane

Horizontal system

The horizontal, or altitude-azimuth, system is based on the position of the observer on Earth, which revolves around its own axis once per sidereal day (23 hours, 56 minutes and 4.091 seconds) in relation to the star background. The positioning of a celestial object by the horizontal system varies with time, but is a useful coordinate system for locating and tracking objects for observers on Earth. It is based on the position of stars relative to an observer's ideal horizon.

Equatorial system

The equatorial coordinate system is centered at Earth's center, but fixed relative to the celestial poles and the March equinox. The coordinates are based on the location of stars relative to Earth's equator if it were projected out to an infinite distance. The equatorial describes the sky as seen from the Solar System, and modern star maps almost exclusively use equatorial coordinates.

The equatorial system is the normal coordinate system for most professional and many amateur astronomers having an equatorial mount that follows the movement of the sky during the night. Celestial objects are found by adjusting the telescope's or other instrument's scales so that they match the equatorial coordinates of the selected object to observe.

Popular choices of pole and equator are the older B1950 and the modern J2000 systems, but a pole and equator "of date" can also be used, meaning one appropriate to the date under consideration, such as when a measurement of the position of a planet or spacecraft is made. There are also subdivisions into "mean of date" coordinates, which average out or ignore nutation, and "true of date," which include nutation.

Ecliptic system

The fundamental plane is the plane of the Earth's orbit, called the ecliptic plane. There are two principal variants of the ecliptic coordinate system: geocentric ecliptic coordinates centered on the Earth and heliocentric ecliptic coordinates centered on the center of mass of the Solar System.

The geocentric ecliptic system was the principal coordinate system for ancient astronomy and is still useful for computing the apparent motions of the Sun, Moon, and planets.^[3]

The heliocentric ecliptic system describes the planets' orbital movement around the Sun, and centers on the barycenter of the Solar System (i.e. very close to the center of the Sun). The system is primarily used for computing the positions of planets and other Solar System bodies, as well as defining their orbital elements.

Galactic system

The galactic coordinate system uses the approximate plane of our galaxy as its fundamental plane. The Solar System is still the center of the coordinate system, and the zero point is defined as the direction towards the galactic center. Galactic latitude resembles the elevation above the galactic plane and galactic longitude determines direction relative to the center of the galaxy.

Supergalactic system

The supergalactic coordinate system corresponds to a fundamental plane that contains a higher than average number of local galaxies in the sky as seen from Earth.

Converting coordinates

Conversions between the various coordinate systems are given.^[4] See the notes before using these equations.

Notation

Horizontal coordinates
- $A$ , azimuth
- $h$ , altitude
Equatorial coordinates
- $α$ , right ascension
- $δ$ , declination
- $ω$ , hour angle
Ecliptic coordinates
- $λ$ , ecliptic longitude
- $β$ , ecliptic latitude
Galactic coordinates
- $l$ , galactic longitude
- $b$ , galactic latitude
Miscellaneous
- $λ o$ , observer's longitude
- $ϕ o$ , observer's latitude
- $ε$ , obliquity of the ecliptic (about 23.4°)
- $θ L$ , local sidereal time
- $θ G$ , Greenwich sidereal time

Hour angle ↔ right ascension

{\begin{aligned}h&=\theta _{\text{L}}-\alpha &&{\mbox{or}}&h&=\theta _{\text{G}}+\lambda _{\text{o}}-\alpha \\\alpha &=\theta _{\text{L}}-h&&{\mbox{or}}&\alpha &=\theta _{\text{G}}+\lambda _{\text{o}}-h\end{aligned}}

Equatorial ↔ ecliptic

The classical equations, derived from spherical trigonometry, for the longitudinal coordinate are presented to the right of a bracket; simply dividing the first equation by the second gives the convenient tangent equation seen on the left.^[5] The rotation matrix equivalent is given beneath each case.^[6] This division is ambiguous because tan has a period of 180° ( $π$ ) whereas cos and sin have periods of 360° (2 $π$ ).

{\begin{aligned}\tan \left(\lambda \right)&={\sin \left(\alpha \right)\cos \left(\varepsilon \right)+\tan \left(\delta \right)\sin \left(\varepsilon \right) \over \cos \left(\alpha \right)};\qquad {\begin{cases}\cos \left(\beta \right)\sin \left(\lambda \right)=\cos \left(\delta \right)\sin \left(\alpha \right)\cos \left(\varepsilon \right)+\sin \left(\delta \right)\sin \left(\varepsilon \right);\\\cos \left(\beta \right)\cos \left(\lambda \right)=\cos \left(\delta \right)\cos \left(\alpha \right).\end{cases}}\\\sin \left(\beta \right)&=\sin \left(\delta \right)\cos \left(\varepsilon \right)-\cos \left(\delta \right)\sin \left(\varepsilon \right)\sin \left(\alpha \right)\\[3pt]{\begin{bmatrix}\cos \left(\beta \right)\cos \left(\lambda \right)\\\cos \left(\beta \right)\sin \left(\lambda \right)\\\sin \left(\beta \right)\end{bmatrix}}&={\begin{bmatrix}1&0&0\\0&\cos \left(\varepsilon \right)&\sin \left(\varepsilon \right)\\0&-\sin \left(\varepsilon \right)&\cos \left(\varepsilon \right)\end{bmatrix}}{\begin{bmatrix}\cos \left(\delta \right)\cos \left(\alpha \right)\\\cos \left(\delta \right)\sin \left(\alpha \right)\\\sin \left(\delta \right)\end{bmatrix}}\\[6pt]\tan \left(\alpha \right)&={\sin \left(\lambda \right)\cos \left(\varepsilon \right)-\tan \left(\beta \right)\sin \left(\varepsilon \right) \over \cos \left(\lambda \right)};\qquad {\begin{cases}\cos \left(\delta \right)\sin \left(\alpha \right)=\cos \left(\beta \right)\sin \left(\lambda \right)\cos \left(\varepsilon \right)-\sin \left(\beta \right)\sin \left(\varepsilon \right);\\\cos \left(\delta \right)\cos \left(\alpha \right)=\cos \left(\beta \right)\cos \left(\lambda \right).\end{cases}}\\[3pt]\sin \left(\delta \right)&=\sin \left(\beta \right)\cos \left(\varepsilon \right)+\cos \left(\beta \right)\sin \left(\varepsilon \right)\sin \left(\lambda \right).\\[6pt]{\begin{bmatrix}\cos \left(\delta \right)\cos \left(\alpha \right)\\\cos \left(\delta \right)\sin \left(\alpha \right)\\\sin \left(\delta \right)\end{bmatrix}}&={\begin{bmatrix}1&0&0\\0&\cos \left(\varepsilon \right)&-\sin \left(\varepsilon \right)\\0&\sin \left(\varepsilon \right)&\cos \left(\varepsilon \right)\end{bmatrix}}{\begin{bmatrix}\cos \left(\beta \right)\cos \left(\lambda \right)\\\cos \left(\beta \right)\sin \left(\lambda \right)\\\sin \left(\beta \right)\end{bmatrix}}.\end{aligned}}

Equatorial ↔ horizontal

Note that azimuth ( $A$ ) is measured from the south point, turning positive to the west.^[7] Zenith distance, the angular distance along the great circle from the zenith to a celestial object, is simply the complementary angle of the altitude: $90° - a$ .^[8]

{\begin{aligned}\tan \left(A\right)&={\sin \left(h\right) \over \cos \left(h\right)\sin \left(\phi _{\text{o}}\right)-\tan \left(\delta \right)\cos \left(\phi _{\text{o}}\right)};\qquad {\begin{cases}\cos \left(a\right)\sin \left(A\right)=\cos \left(\delta \right)\sin \left(h\right);\\\cos \left(a\right)\cos \left(A\right)=\cos \left(\delta \right)\cos \left(h\right)\sin \left(\phi _{\text{o}}\right)-\sin \left(\delta \right)\cos \left(\phi _{\text{o}}\right)\end{cases}}\\[3pt]\sin \left(a\right)&=\sin \left(\phi _{\text{o}}\right)\sin \left(\delta \right)+\cos \left(\phi _{\text{o}}\right)\cos \left(\delta \right)\cos \left(h\right);\end{aligned}}

In solving the $tan(A)$ equation for $A$ , in order to avoid the ambiguity of the arctangent, use of the two-argument arctangent, denoted $arctan(x, y)$ , is recommended. The two-argument arctangent computes the arctangent of $.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num,.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0 0.1em}.mw-parser-output .sfrac .den{border-top:1px solid}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}y/x$ , and accounts for the quadrant in which it is being computed. Thus, consistent with the convention of azimuth being measured from the south and opening positive to the west,

A=-\arctan(x,y)

,

where

{\begin{aligned}x&=-\sin \left(\phi _{\text{o}}\right)\cos \left(\delta \right)\cos \left(h\right)+\cos \left(\phi _{\text{o}}\right)\sin \left(\delta \right)\\y&=\cos \left(\delta \right)\sin \left(h\right)\end{aligned}}

.

If the above formula produces a negative value for $A$ , it can be rendered positive by simply adding 360°.

{\begin{aligned}{\begin{bmatrix}\cos \left(a\right)\cos \left(A\right)\\\cos \left(a\right)\sin \left(A\right)\\\sin \left(a\right)\end{bmatrix}}&={\begin{bmatrix}\sin \left(\phi _{\text{o}}\right)&0&-\cos \left(\phi _{\text{o}}\right)\\0&1&0\\\cos \left(\phi _{\text{o}}\right)&0&\sin \left(\phi _{\text{o}}\right)\end{bmatrix}}{\begin{bmatrix}\cos \left(\delta \right)\cos \left(h\right)\\\cos \left(\delta \right)\sin \left(h\right)\\\sin \left(\delta \right)\end{bmatrix}}\\&={\begin{bmatrix}\sin \left(\phi _{\text{o}}\right)&0&-\cos \left(\phi _{\text{o}}\right)\\0&1&0\\\cos \left(\phi _{\text{o}}\right)&0&\sin \left(\phi _{\text{o}}\right)\end{bmatrix}}{\begin{bmatrix}\cos \left(\theta _{L}\right)&\sin \left(\theta _{L}\right)&0\\\sin \left(\theta _{L}\right)&-\cos \left(\theta _{L}\right)&0\\0&0&1\end{bmatrix}}{\begin{bmatrix}\cos \left(\delta \right)\cos \left(\alpha \right)\\\cos \left(\delta \right)\sin \left(\alpha \right)\\\sin \left(\delta \right)\end{bmatrix}};\\[6pt]\tan \left(h\right)&={\sin \left(A\right) \over \cos \left(A\right)\sin \left(\phi _{\text{o}}\right)+\tan \left(a\right)\cos \left(\phi _{\text{o}}\right)};\qquad {\begin{cases}\cos \left(\delta \right)\sin \left(h\right)=\cos \left(a\right)\sin \left(A\right);\\\cos \left(\delta \right)\cos \left(h\right)=\sin \left(a\right)\cos \left(\phi _{\text{o}}\right)+\cos \left(a\right)\cos \left(A\right)\sin \left(\phi _{\text{o}}\right)\end{cases}}\\[3pt]\sin \left(\delta \right)&=\sin \left(\phi _{\text{o}}\right)\sin \left(a\right)-\cos \left(\phi _{\text{o}}\right)\cos \left(a\right)\cos \left(A\right);\end{aligned}}

^{[lower-alpha 1]}

Again, in solving the $tan(h)$ equation for $h$ , use of the two-argument arctangent that accounts for the quadrant is recommended. Thus, again consistent with the convention of azimuth being measured from the south and opening positive to the west,

h=\arctan(x,y)

,

where

{\begin{aligned}x&=\sin \left(\phi _{\text{o}}\right)\cos \left(a\right)\cos \left(A\right)+\cos \left(\phi _{\text{o}}\right)\sin \left(a\right)\\y&=\cos \left(a\right)\sin \left(A\right)\\[3pt]{\begin{bmatrix}\cos \left(\delta \right)\cos \left(h\right)\\\cos \left(\delta \right)\sin \left(h\right)\\\sin \left(\delta \right)\end{bmatrix}}&={\begin{bmatrix}\sin \left(\phi _{\text{o}}\right)&0&\cos \left(\phi _{\text{o}}\right)\\0&1&0\\-\cos \left(\phi _{\text{o}}\right)&0&\sin \left(\phi _{\text{o}}\right)\end{bmatrix}}{\begin{bmatrix}\cos \left(a\right)\cos \left(A\right)\\\cos \left(a\right)\sin \left(A\right)\\\sin \left(a\right)\end{bmatrix}}\\{\begin{bmatrix}\cos \left(\delta \right)\cos \left(\alpha \right)\\\cos \left(\delta \right)\sin \left(\alpha \right)\\\sin \left(\delta \right)\end{bmatrix}}&={\begin{bmatrix}\cos \left(\theta _{L}\right)&\sin \left(\theta _{L}\right)&0\\\sin \left(\theta _{L}\right)&-\cos \left(\theta _{L}\right)&0\\0&0&1\end{bmatrix}}{\begin{bmatrix}\sin \left(\phi _{\text{o}}\right)&0&\cos \left(\phi _{\text{o}}\right)\\0&1&0\\-\cos \left(\phi _{\text{o}}\right)&0&\sin \left(\phi _{\text{o}}\right)\end{bmatrix}}{\begin{bmatrix}\cos \left(a\right)\cos \left(A\right)\\\cos \left(a\right)\sin \left(A\right)\\\sin \left(a\right)\end{bmatrix}}.\end{aligned}}

Equatorial ↔ galactic

These equations^[14] are for converting equatorial coordinates to Galactic coordinates.

{\begin{aligned}\cos \left(l_{\text{NCP}}-l\right)\cos(b)&=\sin \left(\delta \right)\cos \left(\delta _{\text{G}}\right)-\cos \left(\delta \right)\sin \left(\delta _{\text{G}}\right)\cos \left(\alpha -\alpha _{\text{G}}\right)\\\sin \left(l_{\text{NCP}}-l\right)\cos(b)&=\cos(\delta )\sin \left(\alpha -\alpha _{\text{G}}\right)\\\sin \left(b\right)&=\sin \left(\delta \right)\sin \left(\delta _{\text{G}}\right)+\cos \left(\delta \right)\cos \left(\delta _{\text{G}}\right)\cos \left(\alpha -\alpha _{\text{G}}\right)\end{aligned}}

$\alpha _{\text{G}},\delta _{\text{G}}$ are the equatorial coordinates of the North Galactic Pole and $l_{\text{NCP}}$ is the Galactic longitude of the North Celestial Pole. Referred to J2000.0 the values of these quantities are:

\alpha _{G}=192.85948^{\circ }\qquad \delta _{G}=27.12825^{\circ }\qquad l_{\text{NCP}}=122.93192^{\circ }

If the equatorial coordinates are referred to another equinox, they must be precessed to their place at J2000.0 before applying these formulae.

These equations convert to equatorial coordinates referred to B2000.0.

{\begin{aligned}\sin \left(\alpha -\alpha _{\text{G}}\right)\cos \left(\delta \right)&=\cos \left(b\right)\sin \left(l_{\text{NCP}}-l\right)\\\cos \left(\alpha -\alpha _{\text{G}}\right)\cos \left(\delta \right)&=\sin \left(b\right)\cos \left(\delta _{\text{G}}\right)-\cos \left(b\right)\sin \left(\delta _{\text{G}}\right)\cos \left(l_{\text{NCP}}-l\right)\\\sin \left(\delta \right)&=\sin \left(b\right)\sin \left(\delta _{\text{G}}\right)+\cos \left(b\right)\cos \left(\delta _{\text{G}}\right)\cos \left(l_{\text{NCP}}-l\right)\end{aligned}}

Notes on conversion

Angles in the degrees ( ° ), minutes ( ′ ), and seconds ( ″ ) of sexagesimal measure must be converted to decimal before calculations are performed. Whether they are converted to decimal degrees or radians depends upon the particular calculating machine or program. Negative angles must be carefully handled; –10° 20′ 30″ must be converted as −10° −20′ −30″.
Angles in the hours ( ^h ), minutes ( ^m ), and seconds ( ^s ) of time measure must be converted to decimal degrees or radians before calculations are performed. 1^h = 15°; 1^m = 15′; 1^s = 15″
Angles greater than 360° (2 $π$ ) or less than 0° may need to be reduced to the range 0°−360° (0–2 $π$ ) depending upon the particular calculating machine or program.
The cosine of a latitude (declination, ecliptic and Galactic latitude, and altitude) are never negative by definition, since the latitude varies between −90° and +90°.
Inverse trigonometric functions arcsine, arccosine and arctangent are quadrant-ambiguous, and results should be carefully evaluated. Use of the second arctangent function (denoted in computing as atn2(y,x) or atan2(y,x), which calculates the arctangent of $y / x$ using the sign of both arguments to determine the right quadrant) is recommended when calculating longitude/right ascension/azimuth. An equation which finds the sine, followed by the arcsin function, is recommended when calculating latitude/declination/altitude.
Azimuth ( $A$ ) is referred here to the south point of the horizon, the common astronomical reckoning. An object on the meridian to the south of the observer has $A$ = $h$ = 0° with this usage. However, n Astropy's AltAz, in the Large Binocular Telescope FITS file convention, in XEphem, in the IAU library Standards of Fundamental Astronomy and Section B of the Astronomical Almanac for example, the azimuth is East of North. In navigation and some other disciplines, azimuth is figured from the north.
The equations for altitude ( $a$ ) do not account for atmospheric refraction.
The equations for horizontal coordinates do not account for diurnal parallax, that is, the small offset in the position of a celestial object caused by the position of the observer on the Earth's surface. This effect is significant for the Moon, less so for the planets, minute for stars or more distant objects.
Observer's longitude ( $λ o$ ) here is measured positively westward from the prime meridian; this is contrary to current IAU standards.

Notes

↑ Depending on the azimuth convention in use, the signs of $cos A$ and $sin A$ appear in all four different combinations. Karttunen et al.,^[9] Taff,^[10] and Roth^[11] define $A$ clockwise from the south. Lang^[12] defines it north through east, Smart^[13] north through west. Meeus (1991),^[4] p. 89: $sin δ = sin φ sin a - cos φ cos a cos A$ ; Explanatory Supplement (1961),^[5] p. 26: $sin δ = sin a sin φ + cos a cos A cos φ$ .

Related Research Articles

Angular displacement of a body is the angle in radians, degrees or revolutions through which a point revolves around a centre or a specified axis in a specified sense. When a body rotates about its axis, the motion cannot simply be analyzed as a particle, as in circular motion it undergoes a changing velocity and acceleration at any time (t). When dealing with the rotation of a body, it becomes simpler to consider the body itself rigid. A body is generally considered rigid when the separations between all the particles remains constant throughout the body's motion, so for example parts of its mass are not flying off. In a realistic sense, all things can be deformable, however this impact is minimal and negligible. Thus the rotation of a rigid body over a fixed axis is referred to as rotational motion.

Linear elasticity is a mathematical model of how solid objects deform and become internally stressed due to prescribed loading conditions. It is a simplification of the more general nonlinear theory of elasticity and a branch of continuum mechanics.

In the calculus of variations, a field of mathematical analysis, the functional derivative relates a change in a Functional to a change in a function on which the functional depends.

In geodesy, conversion among different geographic coordinate systems is made necessary by the different geographic coordinate systems in use across the world and over time. Coordinate conversion is composed of a number of different types of conversion: format change of geographic coordinates, conversion of coordinate systems, or transformation to different geodetic datums. Geographic coordinate conversion has applications in cartography, surveying, navigation and geographic information systems.

In probability theory, the Borel–Kolmogorov paradox is a paradox relating to conditional probability with respect to an event of probability zero. It is named after Émile Borel and Andrey Kolmogorov.

A granular material is a conglomeration of discrete solid, macroscopic particles characterized by a loss of energy whenever the particles interact. The constituents that compose granular material are large enough such that they are not subject to thermal motion fluctuations. Thus, the lower size limit for grains in granular material is about 1 μm. On the upper size limit, the physics of granular materials may be applied to ice floes where the individual grains are icebergs and to asteroid belts of the Solar System with individual grains being asteroids.

Propagator Function in quantum field theory showing probability amplitudes of moving particles

In quantum mechanics and quantum field theory, the propagator is a function that specifies the probability amplitude for a particle to travel from one place to another in a given period of time, or to travel with a certain energy and momentum. In Feynman diagrams, which serve to calculate the rate of collisions in quantum field theory, virtual particles contribute their propagator to the rate of the scattering event described by the respective diagram. These may also be viewed as the inverse of the wave operator appropriate to the particle, and are, therefore, often called (causal) Green's functions.

In physics, the Hamilton–Jacobi equation, named after William Rowan Hamilton and Carl Gustav Jacob Jacobi, is an alternative formulation of classical mechanics, equivalent to other formulations such as Newton's laws of motion, Lagrangian mechanics and Hamiltonian mechanics. The Hamilton–Jacobi equation is particularly useful in identifying conserved quantities for mechanical systems, which may be possible even when the mechanical problem itself cannot be solved completely.

The solar zenith angle is the angle between the sun’s rays and the vertical direction. It is closely related to the solar altitude angle, which is the angle between the sun’s rays and a horizontal plane. Since these two angles are complementary, the cosine of either one of them equals the sine of the other. They can both be calculated with the same formula, using results from spherical trigonometry. At solar noon, the zenith angle is at a minimum and is equal to latitude minus solar declination angle. This is the basis by which ancient mariners navigated the oceans.

The Havriliak–Negami relaxation is an empirical modification of the Debye relaxation model in electromagnetism. Unlike the Debye model, the Havriliak–Negami relaxation accounts for the asymmetry and broadness of the dielectric dispersion curve. The model was first used to describe the dielectric relaxation of some polymers, by adding two exponential parameters to the Debye equation:

In particle physics, neutral particle oscillation is the transmutation of a particle with zero electric charge into another neutral particle due to a change of a non-zero internal quantum number, via an interaction that does not conserve that quantum number.

In general relativity, the Gibbons–Hawking–York boundary term is a term that needs to be added to the Einstein–Hilbert action when the underlying spacetime manifold has a boundary.

In mathematics, more specifically in dynamical systems, the method of averaging exploits systems containing time-scales separation: a fast oscillationversus a slow drift. It suggests that we perform an averaging over a given amount of time in order to iron out the fast oscillations and observe the qualitative behavior from the resulting dynamics. The approximated solution holds under finite time inversely proportional to the parameter denoting the slow time scale. It turns out to be a customary problem where there exists the trade off between how good is the approximated solution balanced by how much time it holds to be close to the original solution.

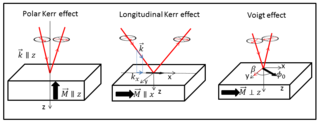
The Voigt effect is a magneto-optical phenomenon which rotates and elliptizes linearly polarised light sent into an optically active medium. Unlike many other magneto-optical effects such as the Kerr or Faraday effect which are linearly proportional to the magnetization, the Voigt effect is proportional to the square of the magnetization and can be seen experimentally at normal incidence. There are several denominations for this effect in the literature: the Cotton–Mouton effect, the Voigt effect, and magnetic-linear birefringence. This last denomination is closer in the physical sense, where the Voigt effect is a magnetic birefringence of the material with an index of refraction parallel and perpendicular $) to the magnetization vector or to the applied magnetic field.$

The Newman–Penrose (NP) formalism is a set of notation developed by Ezra T. Newman and Roger Penrose for general relativity (GR). Their notation is an effort to treat general relativity in terms of spinor notation, which introduces complex forms of the usual variables used in GR. The NP formalism is itself a special case of the tetrad formalism, where the tensors of the theory are projected onto a complete vector basis at each point in spacetime. Usually this vector basis is chosen to reflect some symmetry of the spacetime, leading to simplified expressions for physical observables. In the case of the NP formalism, the vector basis chosen is a null tetrad: a set of four null vectors—two real, and a complex-conjugate pair. The two real members asymptotically point radially inward and radially outward, and the formalism is well adapted to treatment of the propagation of radiation in curved spacetime. The Weyl scalars, derived from the Weyl tensor, are often used. In particular, it can be shown that one of these scalars— $in the appropriate frame—encodes the outgoing gravitational radiation of an asymptotically flat system.$

In mathematics, the dual quaternions are an 8-dimensional real algebra isomorphic to the tensor product of the quaternions and the dual numbers. Thus, they may be constructed in the same way as the quaternions, except using dual numbers instead of real numbers as coefficients. A dual quaternion can be represented in the form A + εB, where A and B are ordinary quaternions and ε is the dual unit, which satisfies ε² = 0 and commutes with every element of the algebra. Unlike quaternions, the dual quaternions do not form a division algebra.

In general relativity, a point mass deflects a light ray with impact parameter $by an angle approximately equal to$

In physics, deformation is the continuum mechanics transformation of a body from a reference configuration to a current configuration. A configuration is a set containing the positions of all particles of the body.

In spherical astronomy, the parallactic angle is the angle between the great circle through a celestial object and the zenith, and the hour circle of the object. It is usually denoted q. In the triangle zenith—object—celestial pole, the parallactic angle will be the position angle of the zenith at the celestial object. Despite its name, this angle is unrelated with parallax. The parallactic angle is zero or 180° when the object crosses the meridian.

The table of chords, created by the Greek astronomer, geometer, and geographer Ptolemy in Egypt during the 2nd century AD, is a trigonometric table in Book I, chapter 11 of Ptolemy's Almagest, a treatise on mathematical astronomy. It is essentially equivalent to a table of values of the sine function. It was the earliest trigonometric table extensive enough for many practical purposes, including those of astronomy. Centuries passed before more extensive trigonometric tables were created. One such table is the Canon Sinuum created at the end of the 16th century.

References

↑ Kanas, Nick. "Star and Solar System Maps: A History of Celestial Cartography". AAS. 5 (4). doi:10.3847/2515-5172/abf35c.
↑ Majewski, Steve. "Coordinate Systems". UVa Department of Astronomy. Archived from the original on 12 March 2016. Retrieved 19 March 2011.
↑ Aaboe, Asger. 2001 Episodes from the Early History of Astronomy. New York: Springer-Verlag., pp. 17–19.
↑ Meeus, Jean (1991). Astronomical Algorithms. Willmann-Bell, Inc., Richmond, VA. ISBN 0-943396-35-2., chap. 12
↑ U.S. Naval Observatory, Nautical Almanac Office; H.M. Nautical Almanac Office (1961). Explanatory Supplement to the Astronomical Ephemeris and the American Ephemeris and Nautical Almanac. H.M. Stationery Office, London., sec. 2A
↑ U.S. Naval Observatory, Nautical Almanac Office (1992). P. Kenneth Seidelmann (ed.). Explanatory Supplement to the Astronomical Almanac. University Science Books, Mill Valley, CA. ISBN 0-935702-68-7., section 11.43
↑ Montenbruck, Oliver; Pfleger, Thomas (2000). Astronomy on the Personal Computer. Springer-Verlag Berlin Heidelberg. ISBN 978-3-540-67221-0., pp 35-37
↑ U.S. Naval Observatory, Nautical Almanac Office; U.K. Hydrographic Office, H.M. Nautical Almanac Office (2008). The Astronomical Almanac for the Year 2010. U.S. Govt. Printing Office. p. M18. ISBN 978-0160820083.
Karttunen, H.; Kröger, P.; Oja, H.; Poutanen, M.; Donner, H. J. (2006). Fundamental Astronomy (5 ed.). Bibcode:2003fuas.book.....K. ISBN 978-3-540-34143-7.
Taff, L. G. (1981). Computational spherical astronomy. Wiley. Bibcode:1981csa..book.....T. ISBN 0-471-06257-X.
Roth, G. D. (23 October 1989). Handbuch für Sternenfreunde. Springer. ISBN 3-540-19436-3.
Lang, Kenneth R. (1978). Astrophysical Formulae. Springer. Bibcode:1978afcp.book.....L. ISBN 3-540-09064-9.
Smart, William Marshall (1949). Text-book on spherical astronomy. Cambridge University Press. Bibcode:1965tbsa.book.....S.
↑ Poleski, Radosław (2013). "Transformation of the equatorial proper motion to the Galactic system". arXiv: 1306.2945 [astro-ph.IM].

External links

NOVAS, the U.S. Naval Observatory's Vector Astrometry Software, an integrated package of subroutines and functions for computing various commonly needed quantities in positional astronomy.
SOFA, the IAU's Standards of Fundamental Astronomy, an accessible and authoritative set of algorithms and procedures that implement standard models used in fundamental astronomy.
This article was originally based on Jason Harris' Astroinfo, which comes along with KStars, a KDE Desktop Planetarium for Linux/KDE.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[14] Depending on the azimuth convention in use, the signs of $cos A$ and $sin A$ appear in all four different combinations. Karttunen et al.,^[9] Taff,^[10] and Roth^[11] define $A$ clockwise from the south. Lang^[12] defines it north through east, Smart^[13] north through west. Meeus (1991),^[4] p. 89: $sin δ = sin φ sin a - cos φ cos a cos A$ ; Explanatory Supplement (1961),^[5] p. 26: $sin δ = sin a sin φ + cos a cos A cos φ$ .

[1] Kanas, Nick. "Star and Solar System Maps: A History of Celestial Cartography". AAS. 5 (4). doi:10.3847/2515-5172/abf35c.

[2] Majewski, Steve. "Coordinate Systems". UVa Department of Astronomy. Archived from the original on 12 March 2016. Retrieved 19 March 2011.

[3] Aaboe, Asger. 2001 Episodes from the Early History of Astronomy. New York: Springer-Verlag., pp. 17–19.

[Meeus-4] Meeus, Jean (1991). Astronomical Algorithms. Willmann-Bell, Inc., Richmond, VA. ISBN 0-943396-35-2., chap. 12

[ExplSupp-5] U.S. Naval Observatory, Nautical Almanac Office; H.M. Nautical Almanac Office (1961). Explanatory Supplement to the Astronomical Ephemeris and the American Ephemeris and Nautical Almanac. H.M. Stationery Office, London., sec. 2A

[6] U.S. Naval Observatory, Nautical Almanac Office (1992). P. Kenneth Seidelmann (ed.). Explanatory Supplement to the Astronomical Almanac. University Science Books, Mill Valley, CA. ISBN 0-935702-68-7., section 11.43

[7] Montenbruck, Oliver; Pfleger, Thomas (2000). Astronomy on the Personal Computer. Springer-Verlag Berlin Heidelberg. ISBN 978-3-540-67221-0., pp 35-37

[8] U.S. Naval Observatory, Nautical Almanac Office; U.K. Hydrographic Office, H.M. Nautical Almanac Office (2008). The Astronomical Almanac for the Year 2010. U.S. Govt. Printing Office. p. M18. ISBN 978-0160820083.

[Karttunen-9] Karttunen, H.; Kröger, P.; Oja, H.; Poutanen, M.; Donner, H. J. (2006). Fundamental Astronomy (5 ed.). Bibcode:2003fuas.book.....K. ISBN 978-3-540-34143-7.

[Taff-10] Taff, L. G. (1981). Computational spherical astronomy. Wiley. Bibcode:1981csa..book.....T. ISBN 0-471-06257-X.

[Roth-11] Roth, G. D. (23 October 1989). Handbuch für Sternenfreunde. Springer. ISBN 3-540-19436-3.

[Lang-12] Lang, Kenneth R. (1978). Astrophysical Formulae. Springer. Bibcode:1978afcp.book.....L. ISBN 3-540-09064-9.

[Smart-13] Smart, William Marshall (1949). Text-book on spherical astronomy. Cambridge University Press. Bibcode:1965tbsa.book.....S.

[15] Poleski, Radosław (2013). "Transformation of the equatorial proper motion to the Galactic system". arXiv: 1306.2945 [astro-ph.IM].

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[lower-alpha 1]

[14]

[9]

[10]

[11]

[12]

[13]