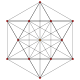
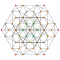
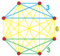
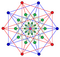
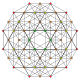
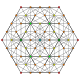
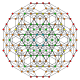
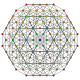
In four-dimensional geometry, a runcinated 5-cell is a convex uniform 4-polytope, being a runcination of the regular 5-cell.

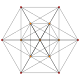
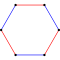
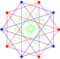
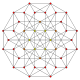
In four-dimensional geometry, the rectified 5-cell is a uniform 4-polytope composed of 5 regular tetrahedral and 5 regular octahedral cells. Each edge has one tetrahedron and two octahedra. Each vertex has two tetrahedra and three octahedra. In total it has 30 triangle faces, 30 edges, and 10 vertices. Each vertex is surrounded by 3 octahedra and 2 tetrahedra; the vertex figure is a triangular prism.

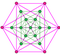
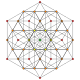
In geometry, a truncated 5-cell is a uniform 4-polytope formed as the truncation of the regular 5-cell.

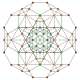
In four-dimensional geometry, a cantellated 5-cell is a convex uniform 4-polytope, being a cantellation of the regular 5-cell.

In geometry, a five-dimensional polytope is a polytope in five-dimensional space, bounded by (4-polytope) facets, pairs of which share a polyhedral cell.
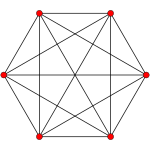
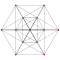
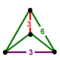
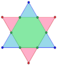
In five-dimensional geometry, a 5-simplex is a self-dual regular 5-polytope. It has six vertices, 15 edges, 20 triangle faces, 15 tetrahedral cells, and 6 5-cell facets. It has a dihedral angle of cos−1(1/5), or approximately 78.46°.

In 7-dimensional geometry, 231 is a uniform polytope, constructed from the E7 group.

In 6-dimensional geometry, the 122 polytope is a uniform polytope, constructed from the E6 group. It was first published in E. L. Elte's 1912 listing of semiregular polytopes, named as V72 (for its 72 vertices).

In 7-dimensional geometry, 132 is a uniform polytope, constructed from the E7 group.

In 8-dimensional geometry, the 142 is a uniform 8-polytope, constructed within the symmetry of the E8 group.

In 7-dimensional geometry, the 321 polytope is a uniform 7-polytope, constructed within the symmetry of the E7 group. It was discovered by Thorold Gosset, published in his 1900 paper. He called it an 7-ic semi-regular figure.
In geometry, the 222 honeycomb is a uniform tessellation of the six-dimensional Euclidean space. It can be represented by the Schläfli symbol {3,3,32,2}. It is constructed from 221 facets and has a 122 vertex figure, with 54 221 polytopes around every vertex.

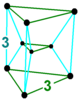
In five-dimensional geometry, a rectified 5-orthoplex is a convex uniform 5-polytope, being a rectification of the regular 5-orthoplex.
In seven-dimensional geometry, a rectified 7-orthoplex is a convex uniform 7-polytope, being a rectification of the regular 7-orthoplex.
In eight-dimensional geometry, a rectified 8-orthoplex is a convex uniform 8-polytope, being a rectification of the regular 8-orthoplex.

In six-dimensional geometry, a rectified 6-orthoplex is a convex uniform 6-polytope, being a rectification of the regular 6-orthoplex.

In six-dimensional geometry, a six-dimensional polytope or 6-polytope is a polytope, bounded by 5-polytope facets.

In seven-dimensional geometry, a rectified 7-simplex is a convex uniform 7-polytope, being a rectification of the regular 7-simplex.
In nine-dimensional geometry, a rectified 9-simplex is a convex uniform 9-polytope, being a rectification of the regular 9-orthoplex.

In nine-dimensional geometry, a rectified 9-simplex is a convex uniform 9-polytope, being a rectification of the regular 9-simplex.