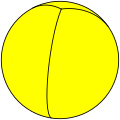
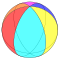
| Spherical tilings (n = 3..5) | ||
|---|---|---|
 *332 |  *432 |  *532 |
| Euclidean plane tiling (n = 6) | ||
 *632 | ||
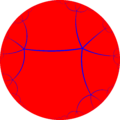
| Hyperbolic plane tilings (n = 7...∞) | ||
 *732 |  *832 |  ... *∞32 |
In geometry, a symmetry mutation is a mapping of fundamental domains between two symmetry groups. [1] They are compactly expressed in orbifold notation. These mutations can occur from spherical tilings to Euclidean tilings to hyperbolic tilings. Hyperbolic tilings can also be divided between compact, paracompact and divergent cases.
Contents
- Mutations of orbifolds
- *n22 symmetry
- Regular tilings
- Prism tilings
- Antiprism tilings
- *n32 symmetry
- Regular tilings 2
- Truncated tilings
- Quasiregular tilings
- Expanded tilings
- Omnitruncated tilings
- Snub tilings
- *n42 symmetry
- Regular tilings 3
- Quasiregular tilings 2
- Truncated tilings 2
- Expanded tilings 2
- Omnitruncated tilings 2
- Snub tilings 2
- *n52 symmetry
- Regular tilings 4
- *n62 symmetry
- Regular tilings 5
- *n82 symmetry
- Regular tilings 6
- References
- Sources
The uniform tilings are the simplest application of these mutations, although more complex patterns can be expressed within a fundamental domain.
This article expressed progressive sequences of uniform tilings within symmetry families.