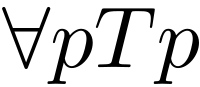
Trivialism is the logical theory that all statements (also known as propositions) are true and, consequently, that all contradictions of the form "p and not p" (e.g. the ball is red and not red) are true. In accordance with this, a trivialist is a person who believes everything is true. [1] [2]
Contents
- Overview
- Etymology
- Theory
- Taxonomy of trivialisms
- Arguments against trivialism
- Aristotle
- Priest
- Arguments for trivialism
- Argument from possibilism
- Paradoxes
- Philosophical implications
- Comparison to skepticism
- Impossibility of action
- Advocates
- Azzouni
- Anaxagoras
- Anti-trivialism
- See also
- References
- Further reading
In classical logic, trivialism is in direct violation of Aristotle's law of noncontradiction. In philosophy, trivialism is considered by some to be the complete opposite of skepticism. Paraconsistent logics may use "the law of non-triviality" to abstain from trivialism in logical practices that involve true contradictions.
Theoretical arguments and anecdotes have been offered for trivialism to contrast it with theories such as modal realism, dialetheism and paraconsistent logics.


