In mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M.

In mathematics, a sequence is an enumerated collection of objects in which repetitions are allowed and order matters. Like a set, it contains members. The number of elements is called the length of the sequence. Unlike a set, the same elements can appear multiple times at different positions in a sequence, and unlike a set, the order does matter. Formally, a sequence can be defined as a function from natural numbers to the elements at each position. The notion of a sequence can be generalized to an indexed family, defined as a function from an arbitrary index set.
In mathematics, the infimum of a subset of a partially ordered set is the greatest element in that is less than or equal to each element of if such an element exists. In other words, it is the greatest element of that is lower or equal to the lowest element of . Consequently, the term greatest lower bound is also commonly used. The supremum of a subset of a partially ordered set is the least element in that is greater than or equal to each element of if such an element exists. In other words, it is the least element of that is greater than or equal to the greatest element of . Consequently, the supremum is also referred to as the least upper bound.

In mathematics, the limit inferior and limit superior of a sequence can be thought of as limiting bounds on the sequence. They can be thought of in a similar fashion for a function. For a set, they are the infimum and supremum of the set's limit points, respectively. In general, when there are multiple objects around which a sequence, function, or set accumulates, the inferior and superior limits extract the smallest and largest of them; the type of object and the measure of size is context-dependent, but the notion of extreme limits is invariant. Limit inferior is also called infimum limit, limit infimum, liminf, inferior limit, lower limit, or inner limit; limit superior is also known as supremum limit, limit supremum, limsup, superior limit, upper limit, or outer limit.
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces. They are sometimes called Lebesgue spaces, named after Henri Lebesgue, although according to the Bourbaki group they were first introduced by Frigyes Riesz.
In the mathematical field of analysis, uniform convergence is a mode of convergence of functions stronger than pointwise convergence, in the sense that the convergence is uniform over the domain. A sequence of functions converges uniformly to a limiting function on a set as the function domain if, given any arbitrarily small positive number , a number can be found such that each of the functions differs from by no more than at every pointin. Described in an informal way, if converges to uniformly, then how quickly the functions approach is "uniform" throughout in the following sense: in order to guarantee that differs from by less than a chosen distance , we only need to make sure that is larger than or equal to a certain , which we can find without knowing the value of in advance. In other words, there exists a number that could depend on but is independent of , such that choosing will ensure that for all . In contrast, pointwise convergence of to merely guarantees that for any given in advance, we can find such that, for that particular, falls within of whenever .

In the mathematical field of numerical analysis, Runge's phenomenon is a problem of oscillation at the edges of an interval that occurs when using polynomial interpolation with polynomials of high degree over a set of equispaced interpolation points. It was discovered by Carl David Tolmé Runge (1901) when exploring the behavior of errors when using polynomial interpolation to approximate certain functions. The discovery shows that going to higher degrees does not always improve accuracy. The phenomenon is similar to the Gibbs phenomenon in Fourier series approximations.
In functional analysis and related areas of mathematics, Fréchet spaces, named after Maurice Fréchet, are special topological vector spaces. They are generalizations of Banach spaces. All Banach and Hilbert spaces are Fréchet spaces. Spaces of infinitely differentiable functions are typical examples of Fréchet spaces, many of which are typically not Banach spaces.
In mathematics, the uniform boundedness principle or Banach–Steinhaus theorem is one of the fundamental results in functional analysis. Together with the Hahn–Banach theorem and the open mapping theorem, it is considered one of the cornerstones of the field. In its basic form, it asserts that for a family of continuous linear operators whose domain is a Banach space, pointwise boundedness is equivalent to uniform boundedness in operator norm.
In mathematics, pointwise convergence is one of various senses in which a sequence of functions can converge to a particular function. It is weaker than uniform convergence, to which it is often compared.
In mathematics, the limit of a sequence of sets is a set whose elements are determined by the sequence in either of two equivalent ways: (1) by upper and lower bounds on the sequence that converge monotonically to the same set and (2) by convergence of a sequence of indicator functions which are themselves real-valued. As is the case with sequences of other objects, convergence is not necessary or even usual.
In measure theory, Lebesgue's dominated convergence theorem provides sufficient conditions under which almost everywhere convergence of a sequence of functions implies convergence in the L1 norm. Its power and utility are two of the primary theoretical advantages of Lebesgue integration over Riemann integration.
The Arzelà–Ascoli theorem is a fundamental result of mathematical analysis giving necessary and sufficient conditions to decide whether every sequence of a given family of real-valued continuous functions defined on a closed and bounded interval has a uniformly convergent subsequence. The main condition is the equicontinuity of the family of functions. The theorem is the basis of many proofs in mathematics, including that of the Peano existence theorem in the theory of ordinary differential equations, Montel's theorem in complex analysis, and the Peter–Weyl theorem in harmonic analysis and various results concerning compactness of integral operators.
In mathematical analysis, a modulus of continuity is a function ω : [0, ∞] → [0, ∞] used to measure quantitatively the uniform continuity of functions. So, a function f : I → R admits ω as a modulus of continuity if and only if
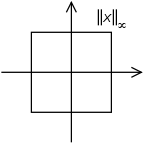
In mathematics, Chebyshev distance, maximum metric, or L∞ metric is a metric defined on a real coordinate space where the distance between two points is the greatest of their differences along any coordinate dimension. It is named after Pafnuty Chebyshev.
In functional analysis and related areas of mathematics, a sequence space is a vector space whose elements are infinite sequences of real or complex numbers. Equivalently, it is a function space whose elements are functions from the natural numbers to the field K of real or complex numbers. The set of all such functions is naturally identified with the set of all possible infinite sequences with elements in K, and can be turned into a vector space under the operations of pointwise addition of functions and pointwise scalar multiplication. All sequence spaces are linear subspaces of this space. Sequence spaces are typically equipped with a norm, or at least the structure of a topological vector space.

In probability theory, Donsker's theorem, named after Monroe D. Donsker, is a functional extension of the central limit theorem for empirical distribution functions. Specifically, the theorem states that an appropriately centered and scaled version of the empirical distribution function converges to a Gaussian process.
In mathematics, more specifically measure theory, there are various notions of the convergence of measures. For an intuitive general sense of what is meant by convergence of measures, consider a sequence of measures μn on a space, sharing a common collection of measurable sets. Such a sequence might represent an attempt to construct 'better and better' approximations to a desired measure μ that is difficult to obtain directly. The meaning of 'better and better' is subject to all the usual caveats for taking limits; for any error tolerance ε > 0 we require there be N sufficiently large for n ≥ N to ensure the 'difference' between μn and μ is smaller than ε. Various notions of convergence specify precisely what the word 'difference' should mean in that description; these notions are not equivalent to one another, and vary in strength.
In mathematics, the conformal radius is a way to measure the size of a simply connected planar domain D viewed from a point z in it. As opposed to notions using Euclidean distance, this notion is well-suited to use in complex analysis, in particular in conformal maps and conformal geometry.
In mathematics, , the vector space of bounded sequences with the supremum norm, and , the vector space of essentially bounded measurable functions with the essential supremum norm, are two closely related Banach spaces. In fact the former is a special case of the latter. As a Banach space they are the continuous dual of the Banach spaces of absolutely summable sequences, and of absolutely integrable measurable functions. Pointwise multiplication gives them the structure of a Banach algebra, and in fact they are the standard examples of abelian Von Neumann algebras.