Calculation of diversity
Species diversity in a dataset can be calculated by first taking the weighted average of species proportional abundances in the dataset, and then taking the inverse of this. The equation is: [1] [2] [3]

The denominator equals mean proportional species abundance in the dataset as calculated with the weighted generalized mean with exponent q - 1. In the equation, S is the total number of species (species richness) in the dataset, and the proportional abundance of the ith species is  . The proportional abundances themselves are used as weights. The equation is often written in the equivalent form:
. The proportional abundances themselves are used as weights. The equation is often written in the equivalent form:

The value of q determines which mean is used. q = 0 corresponds to the weighted harmonic mean, which is 1/S because the  values cancel out, with the result that 0D is equal to the number of species or species richness, S. q = 1 is undefined, except that the limit as q approaches 1 is well defined: [4]
values cancel out, with the result that 0D is equal to the number of species or species richness, S. q = 1 is undefined, except that the limit as q approaches 1 is well defined: [4]

which is the exponential of the Shannon entropy.
q = 2 corresponds to the arithmetic mean. As q approaches infinity, the generalized mean approaches the maximum  value. In practice, q modifies species weighting, such that increasing q increases the weight given to the most abundant species, and fewer equally abundant species are hence needed to reach mean proportional abundance. Consequently, large values of q lead to smaller species diversity than small values of q for the same dataset. If all species are equally abundant in the dataset, changing the value of q has no effect, but species diversity at any value of q equals species richness.
value. In practice, q modifies species weighting, such that increasing q increases the weight given to the most abundant species, and fewer equally abundant species are hence needed to reach mean proportional abundance. Consequently, large values of q lead to smaller species diversity than small values of q for the same dataset. If all species are equally abundant in the dataset, changing the value of q has no effect, but species diversity at any value of q equals species richness.
Negative values of q are not used, because then the effective number of species (diversity) would exceed the actual number of species (richness). As q approaches negative infinity, the generalized mean approaches the minimum  value. In many real datasets, the least abundant species is represented by a single individual, and then the effective number of species would equal the number of individuals in the dataset. [2] [3]
value. In many real datasets, the least abundant species is represented by a single individual, and then the effective number of species would equal the number of individuals in the dataset. [2] [3]
The same equation can be used to calculate the diversity in relation to any classification, not only species. If the individuals are classified into genera or functional types,  represents the proportional abundance of the ith genus or functional type, and qD equals genus diversity or functional type diversity, respectively.
represents the proportional abundance of the ith genus or functional type, and qD equals genus diversity or functional type diversity, respectively.
Diversity indices
Often researchers have used the values given by one or more diversity indices to quantify species diversity. Such indices include species richness, the Shannon index, the Simpson index, and the complement of the Simpson index (also known as the Gini-Simpson index). [5] [6] [7]
When interpreted in ecological terms, each one of these indices corresponds to a different thing, and their values are therefore not directly comparable. Species richness quantifies the actual rather than effective number of species. The Shannon index equals log(1D), that is, q approaching 1, and in practice quantifies the uncertainty in the species identity of an individual that is taken at random from the dataset. The Simpson index equals 1/2D, q = 2, and quantifies the probability that two individuals taken at random from the dataset (with replacement of the first individual before taking the second) represent the same species. The Gini-Simpson index equals 1 - 1/2D and quantifies the probability that the two randomly taken individuals represent different species. [1] [2] [3] [7] [8]
Sampling considerations
Depending on the purposes of quantifying species diversity, the data set used for the calculations can be obtained in different ways. Although species diversity can be calculated for any data-set where individuals have been identified to species, meaningful ecological interpretations require that the dataset is appropriate for the questions at hand. In practice, the interest is usually in the species diversity of areas so large that not all individuals in them can be observed and identified to species, but a sample of the relevant individuals has to be obtained. Extrapolation from the sample to the underlying population of interest is not straightforward, because the species diversity of the available sample generally gives an underestimation of the species diversity in the entire population. Applying different sampling methods will lead to different sets of individuals being observed for the same area of interest, and the species diversity of each set may be different. When a new individual is added to a dataset, it may introduce a species that was not yet represented. How much this increases species diversity depends on the value of q: when q = 0, each new actual species causes species diversity to increase by one effective species, but when q is large, adding a rare species to a dataset has little effect on its species diversity. [9]
In general, sets with many individuals can be expected to have higher species diversity than sets with fewer individuals. When species diversity values are compared among sets, sampling efforts need to be standardised in an appropriate way for the comparisons to yield ecologically meaningful results. Resampling methods can be used to bring samples of different sizes to a common footing. [10] [11] Species discovery curves and the number of species only represented by one or a few individuals can be used to help in estimating how representative the available sample is of the population from which it was drawn. [12] [13]

In economics, the Gini coefficient, also known as the Gini index or Gini ratio, is a measure of statistical dispersion intended to represent the income inequality, the wealth inequality, or the consumption inequality within a nation or a social group. It was developed by Italian statistician and sociologist Corrado Gini.

The unified neutral theory of biodiversity and biogeography is a theory and the title of a monograph by ecologist Stephen P. Hubbell. It aims to explain the diversity and relative abundance of species in ecological communities. Like other neutral theories of ecology, Hubbell assumes that the differences between members of an ecological community of trophically similar species are "neutral", or irrelevant to their success. This implies that niche differences do not influence abundance and the abundance of each species follows a random walk. The theory has sparked controversy, and some authors consider it a more complex version of other null models that fit the data better.

In statistics, the coefficient of determination, denoted R2 or r2 and pronounced "R squared", is the proportion of the variation in the dependent variable that is predictable from the independent variable(s).

Species richness is the number of different species represented in an ecological community, landscape or region. Species richness is simply a count of species, and it does not take into account the abundances of the species or their relative abundance distributions. Species richness is sometimes considered synonymous with species diversity, but the formal metric species diversity takes into account both species richness and species evenness.

In statistics, ordinary least squares (OLS) is a type of linear least squares method for choosing the unknown parameters in a linear regression model by the principle of least squares: minimizing the sum of the squares of the differences between the observed dependent variable in the input dataset and the output of the (linear) function of the independent variable. Some sources consider OLS to be linear regression.
This glossary of statistics and probability is a list of definitions of terms and concepts used in the mathematical sciences of statistics and probability, their sub-disciplines, and related fields. For additional related terms, see Glossary of mathematics and Glossary of experimental design.
A diversity index is a method of measuring how many different types there are in a dataset. Diversity indices are statistical representations of different aspects of biodiversity, which are useful simplifications for comparing different communities or sites.
In ecology, alpha diversity (α-diversity) is the mean species diversity in a site at a local scale. The term was introduced by R. H. Whittaker together with the terms beta diversity (β-diversity) and gamma diversity (γ-diversity). Whittaker's idea was that the total species diversity in a landscape is determined by two different things, the mean species diversity in sites at a more local scale and the differentiation among those sites.
Species evenness describes the commonness or rarity of a species; it requires knowing the abundance of each species relative to those of the other species within the community. Abundance values can be difficult to obtain. Area-based counts, distance methods, and mark–recapture studies are the three general categories of methods for estimating abundance.
In ecology, beta diversity is the ratio between regional and local species diversity. The term was introduced by R. H. Whittaker together with the terms alpha diversity (α-diversity) and gamma diversity (γ-diversity). The idea was that the total species diversity in a landscape (γ) is determined by two different things: the mean species diversity at the local level (α) and the differentiation among local sites (β). Other formulations for beta diversity include "absolute species turnover", "Whittaker's species turnover" and "proportional species turnover".
In ecology, gamma diversity (γ-diversity) is the total species diversity in a landscape. The term was introduced by R. H. Whittaker together with the terms alpha diversity (α-diversity) and beta diversity (β-diversity). Whittaker's idea was that the total species diversity in a landscape (γ) is determined by two different things, the mean species diversity in sites at a more local scale (α) and the differentiation among those sites (β). According to this reasoning, alpha diversity and beta diversity constitute independent components of gamma diversity:
An index of qualitative variation (IQV) is a measure of statistical dispersion in nominal distributions. Examples include the variation ratio or the information entropy.
In probability theory and statistics, the index of dispersion, dispersion index, coefficient of dispersion, relative variance, or variance-to-mean ratio (VMR), like the coefficient of variation, is a normalized measure of the dispersion of a probability distribution: it is a measure used to quantify whether a set of observed occurrences are clustered or dispersed compared to a standard statistical model.
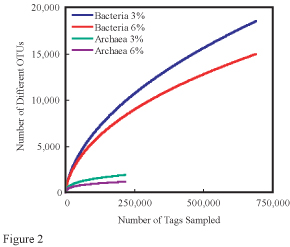
In ecology, rarefaction is a technique to assess species richness from the results of sampling. Rarefaction allows the calculation of species richness for a given number of individual samples, based on the construction of so-called rarefaction curves. This curve is a plot of the number of species as a function of the number of samples. Rarefaction curves generally grow rapidly at first, as the most common species are found, but the curves plateau as only the rarest species remain to be sampled.

The body size-species richness distribution is a pattern observed in the way taxa are distributed over large spatial scales. The number of species that exhibit small body size generally far exceed the number of species that are large-bodied. Macroecology has long sought to understand the mechanisms that underlie the patterns of biodiversity, such as the body size-species richness pattern.
Mechanistic models for niche apportionment are biological models used to explain relative species abundance distributions. These niche apportionment models describe how species break up resource pool in multi-dimensional space, determining the distribution of abundances of individuals among species. The relative abundances of species are usually expressed as a Whittaker plot, or rank abundance plot, where species are ranked by number of individuals on the x-axis, plotted against the log relative abundance of each species on the y-axis. The relative abundance can be measured as the relative number of individuals within species or the relative biomass of individuals within species.
Relative species abundance is a component of biodiversity and is a measure of how common or rare a species is relative to other species in a defined location or community. Relative abundance is the percent composition of an organism of a particular kind relative to the total number of organisms in the area. Relative species abundances tend to conform to specific patterns that are among the best-known and most-studied patterns in macroecology. Different populations in a community exist in relative proportions; this idea is known as relative abundance.
A variety of objective means exist to empirically measure biodiversity. Each measure relates to a particular use of the data, and is likely to be associated with the variety of genes. Biodiversity is commonly measured in terms of taxonomic richness of a geographic area over a time interval. In order to calculate biodiversity, species evenness, species richness, and species diversity are to be obtained first. Species evenness is the relative number of individuals of each species in a given area. Species richness is the number of species present in a given area. Species diversity is the relationship between species evenness and species richness. There are many ways to measure biodiversity within a given ecosystem. However, the two most popular are Shannon-Weaver diversity index, commonly referred to as Shannon diversity index, and the other is Simpsons diversity index. Although many scientists prefer to use Shannon's diversity index simply because it takes into account species richness.
Taylor's power law is an empirical law in ecology that relates the variance of the number of individuals of a species per unit area of habitat to the corresponding mean by a power law relationship. It is named after the ecologist who first proposed it in 1961, Lionel Roy Taylor (1924–2007). Taylor's original name for this relationship was the law of the mean. The name Taylor's law was coined by Southwood in 1966.
In statistics, linear regression is a model that estimates the linear relationship between a scalar response and one or more explanatory variables. A model with exactly one explanatory variable is a simple linear regression; a model with two or more explanatory variables is a multiple linear regression. This term is distinct from multivariate linear regression, which predicts multiple correlated dependent variables rather than a single dependent variable.









