In atomic physics, the Bohr model or Rutherford–Bohr model was the first successful model of the atom. Developed from 1911 to 1918 by Niels Bohr and building on Ernest Rutherford's nuclear model, it supplanted the plum pudding model of J J Thomson only to be replaced by the quantum atomic model in the 1920s. It consists of a small, dense nucleus surrounded by orbiting electrons. It is analogous to the structure of the Solar System, but with attraction provided by electrostatic force rather than gravity, and with the electron energies quantized.

Nuclear fusion is a reaction in which two or more atomic nuclei, usually deuterium and tritium, combine to form one or more different atomic nuclei and subatomic particles. The difference in mass between the reactants and products is manifested as either the release or absorption of energy. This difference in mass arises due to the difference in nuclear binding energy between the atomic nuclei before and after the reaction. Nuclear fusion is the process that powers active or main-sequence stars and other high-magnitude stars, where large amounts of energy are released.

Nuclear fission is a reaction in which the nucleus of an atom splits into two or more smaller nuclei. The fission process often produces gamma photons, and releases a very large amount of energy even by the energetic standards of radioactive decay.

In nuclear physics, the island of stability is a predicted set of isotopes of superheavy elements that may have considerably longer half-lives than known isotopes of these elements. It is predicted to appear as an "island" in the chart of nuclides, separated from known stable and long-lived primordial radionuclides. Its theoretical existence is attributed to stabilizing effects of predicted "magic numbers" of protons and neutrons in the superheavy mass region.
In quantum chemistry and molecular physics, the Born–Oppenheimer (BO) approximation is the best-known mathematical approximation in molecular dynamics. Specifically, it is the assumption that the wave functions of atomic nuclei and electrons in a molecule can be treated separately, based on the fact that the nuclei are much heavier than the electrons. Due to the larger relative mass of a nucleus compared to an electron, the coordinates of the nuclei in a system are approximated as fixed, while the coordinates of the electrons are dynamic. The approach is named after Max Born and his 23-year-old graduate student J. Robert Oppenheimer, the latter of whom proposed it in 1927 during a period of intense fervent in the development of quantum mechanics.
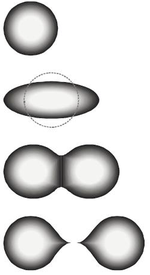
In nuclear physics a superdeformed nucleus is a nucleus that is very far from spherical, forming an ellipsoid with axes in ratios of approximately 2:1:1. Normal deformation is approximately 1.3:1:1. Only some nuclei can exist in superdeformed states.

The Rutherford scattering experiments were a landmark series of experiments by which scientists learned that every atom has a nucleus where all of its positive charge and most of its mass is concentrated. They deduced this after measuring how an alpha particle beam is scattered when it strikes a thin metal foil. The experiments were performed between 1906 and 1913 by Hans Geiger and Ernest Marsden under the direction of Ernest Rutherford at the Physical Laboratories of the University of Manchester.

Spontaneous fission (SF) is a form of radioactive decay in which a heavy atomic nucleus splits into two or more lighter nuclei. In contrast to induced fission, there is no inciting particle to trigger the decay; it is a purely probabilistic process.

In atomic physics, hyperfine structure is defined by small shifts in otherwise degenerate electronic energy levels and the resulting splittings in those electronic energy levels of atoms, molecules, and ions, due to electromagnetic multipole interaction between the nucleus and electron clouds.

In nuclear physics, the semi-empirical mass formula (SEMF) is used to approximate the mass of an atomic nucleus from its number of protons and neutrons. As the name suggests, it is based partly on theory and partly on empirical measurements. The formula represents the liquid-drop model proposed by George Gamow, which can account for most of the terms in the formula and gives rough estimates for the values of the coefficients. It was first formulated in 1935 by German physicist Carl Friedrich von Weizsäcker, and although refinements have been made to the coefficients over the years, the structure of the formula remains the same today.

Cluster decay, also named heavy particle radioactivity, heavy ion radioactivity or heavy cluster decay, is a rare type of nuclear decay in which an atomic nucleus emits a small "cluster" of neutrons and protons, more than in an alpha particle, but less than a typical binary fission fragment. Ternary fission into three fragments also produces products in the cluster size. The loss of protons from the parent nucleus changes it to the nucleus of a different element, the daughter, with a mass number Ad = A − Ae and atomic number Zd = Z − Ze, where Ae = Ne + Ze. For example:
Nuclear reactor physics is the field of physics that studies and deals with the applied study and engineering applications of chain reaction to induce a controlled rate of fission in a nuclear reactor for the production of energy. Most nuclear reactors use a chain reaction to induce a controlled rate of nuclear fission in fissile material, releasing both energy and free neutrons. A reactor consists of an assembly of nuclear fuel, usually surrounded by a neutron moderator such as regular water, heavy water, graphite, or zirconium hydride, and fitted with mechanisms such as control rods which control the rate of the reaction.
In atomic, molecular, and optical physics and quantum chemistry, the molecular Hamiltonian is the Hamiltonian operator representing the energy of the electrons and nuclei in a molecule. This operator and the associated Schrödinger equation play a central role in computational chemistry and physics for computing properties of molecules and aggregates of molecules, such as thermal conductivity, specific heat, electrical conductivity, optical, and magnetic properties, and reactivity.
Alpha spectrometry is the quantitative study of the energy of alpha particles emitted by a radioactive nuclide that is an alpha emitter.

In nuclear physics, the valley of stability is a characterization of the stability of nuclides to radioactivity based on their binding energy. Nuclides are composed of protons and neutrons. The shape of the valley refers to the profile of binding energy as a function of the numbers of neutrons and protons, with the lowest part of the valley corresponding to the region of most stable nuclei. The line of stable nuclides down the center of the valley of stability is known as the line of beta stability. The sides of the valley correspond to increasing instability to beta decay. The decay of a nuclide becomes more energetically favorable the further it is from the line of beta stability. The boundaries of the valley correspond to the nuclear drip lines, where nuclides become so unstable they emit single protons or single neutrons. Regions of instability within the valley at high atomic number also include radioactive decay by alpha radiation or spontaneous fission. The shape of the valley is roughly an elongated paraboloid corresponding to the nuclide binding energies as a function of neutron and atomic numbers.
The Gamow factor, Sommerfeld factor or Gamow–Sommerfeld factor, named after its discoverer George Gamow or after Arnold Sommerfeld, is a probability factor for two nuclear particles' chance of overcoming the Coulomb barrier in order to undergo nuclear reactions, for example in nuclear fusion. By classical physics, there is almost no possibility for protons to fuse by crossing each other's Coulomb barrier at temperatures commonly observed to cause fusion, such as those found in the Sun. When George Gamow instead applied quantum mechanics to the problem, he found that there was a significant chance for the fusion due to tunneling.

The neutron–proton ratio of an atomic nucleus is the ratio of its number of neutrons to its number of protons. Among stable nuclei and naturally occurring nuclei, this ratio generally increases with increasing atomic number. This is because electrical repulsive forces between protons scale with distance differently than strong nuclear force attractions. In particular, most pairs of protons in large nuclei are not far enough apart, such that electrical repulsion dominates over the strong nuclear force, and thus proton density in stable larger nuclei must be lower than in stable smaller nuclei where more pairs of protons have appreciable short-range nuclear force attractions.
Unbiquadium, also known as element 124 or eka-uranium, is a hypothetical chemical element; it has placeholder symbol Ubq and atomic number 124. Unbiquadium and Ubq are the temporary IUPAC name and symbol, respectively, until the element is discovered, confirmed, and a permanent name is decided upon. In the periodic table, unbiquadium is expected to be a g-block superactinide and the sixth element in the 8th period. Unbiquadium has attracted attention, as it may lie within the island of stability, leading to longer half-lives, especially for 308Ubq which is predicted to have a magic number of neutrons (184).
The Nilsson model is a nuclear shell model treating the atomic nucleus as a deformed sphere. In 1953, the first experimental examples were found of rotational bands in nuclei, with their energy levels following the same J(J+1) pattern of energies as in rotating molecules. Quantum mechanically, it is impossible to have a collective rotation of a sphere, so this implied that the shape of these nuclei was nonspherical. In principle, these rotational states could have been described as coherent superpositions of particle-hole excitations in the basis consisting of single-particle states of the spherical potential. But in reality, the description of these states in this manner is intractable, due to the large number of valence particles—and this intractability was even greater in the 1950s, when computing power was extremely rudimentary. For these reasons, Aage Bohr, Ben Mottelson, and Sven Gösta Nilsson constructed models in which the potential was deformed into an ellipsoidal shape. The first successful model of this type is the one now known as the Nilsson model. It is essentially a nuclear shell model using a harmonic oscillator potential, but with anisotropy added, so that the oscillator frequencies along the three Cartesian axes are not all the same. Typically the shape is a prolate ellipsoid, with the axis of symmetry taken to be z.
In a nuclear weapon, a tamper is an optional layer of dense material surrounding the fissile material. It is used in nuclear weapon design to reduce the critical mass and to delay the expansion of the reacting material through its inertia, which delays the thermal expansion of the fissioning fuel mass, keeping it supercritical longer. Often the same layer serves both as tamper and as neutron reflector. The weapon disintegrates as the reaction proceeds, and this stops the reaction, so the use of a tamper makes for a longer-lasting, more energetic and more efficient explosion. The yield can be further enhanced using a fissionable tamper.