
In physics, the Navier–Stokes equations are certain partial differential equations which describe the motion of viscous fluid substances, named after French engineer and physicist Claude-Louis Navier and Anglo-Irish physicist and mathematician George Gabriel Stokes. They were developed over several decades of progressively building the theories, from 1822 (Navier) to 1842–1850 (Stokes).
The Klein–Gordon equation is a relativistic wave equation, related to the Schrödinger equation. It is second-order in space and time and manifestly Lorentz-covariant. It is a quantized version of the relativistic energy–momentum relation. Its solutions include a quantum scalar or pseudoscalar field, a field whose quanta are spinless particles. Its theoretical relevance is similar to that of the Dirac equation. Electromagnetic interactions can be incorporated, forming the topic of scalar electrodynamics, but because common spinless particles like the pions are unstable and also experience the strong interaction the practical utility is limited.
Linear elasticity is a mathematical model of how solid objects deform and become internally stressed due to prescribed loading conditions. It is a simplification of the more general nonlinear theory of elasticity and a branch of continuum mechanics.

In mathematics, theta functions are special functions of several complex variables. They are important in many areas, including the theories of Abelian varieties and moduli spaces, and of quadratic forms. They have also been applied to soliton theory. When generalized to a Grassmann algebra, they also appear in quantum field theory.

In mathematics, Felix Klein's j-invariant or j function, regarded as a function of a complex variable τ, is a modular function of weight zero for SL(2, Z) defined on the upper half-plane of complex numbers. It is the unique such function which is holomorphic away from a simple pole at the cusp such that
The Nambu–Goto action is the simplest invariant action in bosonic string theory, and is also used in other theories that investigate string-like objects. It is the starting point of the analysis of zero-thickness string behavior, using the principles of Lagrangian mechanics. Just as the action for a free point particle is proportional to its proper time — i.e., the "length" of its world-line — a relativistic string's action is proportional to the area of the sheet which the string traces as it travels through spacetime.
In physics, the Polyakov action is an action of the two-dimensional conformal field theory describing the worldsheet of a string in string theory. It was introduced by Stanley Deser and Bruno Zumino and independently by L. Brink, P. Di Vecchia and P. S. Howe in 1976, and has become associated with Alexander Polyakov after he made use of it in quantizing the string in 1981. The action reads
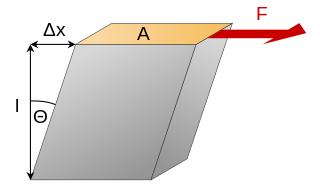
In materials science, shear modulus or modulus of rigidity, denoted by G, or sometimes S or μ, is a measure of the elastic shear stiffness of a material and is defined as the ratio of shear stress to the shear strain:

A theoretical motivation for general relativity, including the motivation for the geodesic equation and the Einstein field equation, can be obtained from special relativity by examining the dynamics of particles in circular orbits about the earth. A key advantage in examining circular orbits is that it is possible to know the solution of the Einstein Field Equation a priori. This provides a means to inform and verify the formalism.
In physics and fluid mechanics, a Blasius boundary layer describes the steady two-dimensional laminar boundary layer that forms on a semi-infinite plate which is held parallel to a constant unidirectional flow. Falkner and Skan later generalized Blasius' solution to wedge flow, i.e. flows in which the plate is not parallel to the flow.
Bilinear time–frequency distributions, or quadratic time–frequency distributions, arise in a sub-field of signal analysis and signal processing called time–frequency signal processing, and, in the statistical analysis of time series data. Such methods are used where one needs to deal with a situation where the frequency composition of a signal may be changing over time; this sub-field used to be called time–frequency signal analysis, and is now more often called time–frequency signal processing due to the progress in using these methods to a wide range of signal-processing problems.

The Rogers–Ramanujan continued fraction is a continued fraction discovered by Rogers (1894) and independently by Srinivasa Ramanujan, and closely related to the Rogers–Ramanujan identities. It can be evaluated explicitly for a broad class of values of its argument.

In fluid dynamics, a cnoidal wave is a nonlinear and exact periodic wave solution of the Korteweg–de Vries equation. These solutions are in terms of the Jacobi elliptic function cn, which is why they are coined cnoidal waves. They are used to describe surface gravity waves of fairly long wavelength, as compared to the water depth.
In general relativity, the Vaidya metric describes the non-empty external spacetime of a spherically symmetric and nonrotating star which is either emitting or absorbing null dusts. It is named after the Indian physicist Prahalad Chunnilal Vaidya and constitutes the simplest non-static generalization of the non-radiative Schwarzschild solution to Einstein's field equation, and therefore is also called the "radiating(shining) Schwarzschild metric".
The table of chords, created by the Greek astronomer, geometer, and geographer Ptolemy in Egypt during the 2nd century AD, is a trigonometric table in Book I, chapter 11 of Ptolemy's Almagest, a treatise on mathematical astronomy. It is essentially equivalent to a table of values of the sine function. It was the earliest trigonometric table extensive enough for many practical purposes, including those of astronomy. Centuries passed before more extensive trigonometric tables were created. One such table is the Canon Sinuum created at the end of the 16th century.
In mathematical physics, the Belinfante–Rosenfeld tensor is a modification of the energy–momentum tensor that is constructed from the canonical energy–momentum tensor and the spin current so as to be symmetric yet still conserved.
In mathematics, the Weber modular functions are a family of three functions f, f1, and f2, studied by Heinrich Martin Weber.
Exponential Tilting (ET), Exponential Twisting, or Exponential Change of Measure (ECM) is a distribution shifting technique used in many parts of mathematics. The different exponential tiltings of a random variable is known as the natural exponential family of .
In fluid dynamics, Rayleigh problem also known as Stokes first problem is a problem of determining the flow created by a sudden movement of an infinitely long plate from rest, named after Lord Rayleigh and Sir George Stokes. This is considered as one of the simplest unsteady problem that have exact solution for the Navier-Stokes equations. The impulse movement of semi-infinite plate was studied by Keith Stewartson.
A proper reference frame in the theory of relativity is a particular form of accelerated reference frame, that is, a reference frame in which an accelerated observer can be considered as being at rest. It can describe phenomena in curved spacetime, as well as in "flat" Minkowski spacetime in which the spacetime curvature caused by the energy–momentum tensor can be disregarded. Since this article considers only flat spacetime—and uses the definition that special relativity is the theory of flat spacetime while general relativity is a theory of gravitation in terms of curved spacetime—it is consequently concerned with accelerated frames in special relativity.





















































































