Kynea number

Last updated October 29, 2020

A Kynea number is an integer of the form

4^{n}+2^{n+1}-1

.

An equivalent formula is

(2^{n}+1)^{2}-2

.

This indicates that a Kynea number is the nth power of 4 plus the (n + 1)th Mersenne number. Kynea numbers were studied by Cletus Emmanuel who named them after a baby girl.^[1]

Properties

The binary representation of the nth Kynea number is a single leading one, followed by n - 1 consecutive zeroes, followed by n + 1 consecutive ones, or to put it algebraically:

4^{n}+\sum _{i=0}^{n}2^{i}.

So, for example, 23 is 10111 in binary, 79 is 1001111, etc. The difference between the nth Kynea number and the nth Carol number is the (n + 2)th power of two.

Prime Kynea numbers

Starting with 7, every third Kynea number is a multiple of 7. Thus, for a Kynea number to be a prime number, its index n cannot be of the form 3x + 1 for x > 0. The first few Kynea numbers that are also prime are 7, 23, 79, 1087, 66047, 263167, 16785407 (sequence A091514 in the OEIS ).

Their n values are: 1, 2, 3, 5, 8, 9, 12, 15, 17, 18, 21, 23, 27, 32, 51, 65, 87, 180, 242, 467, ... (sequence A091513 in the OEIS ).

As of July 2019^[update], the largest known prime Kynea number has index n = 852770, which has 513419 digits.^[2]^[3] It was found by Ryan Propper in July 2019 using the programs CKSieve and PrimeFormGW. It is the 51st Kynea prime.

Related Research Articles

Fibonacci number Integer in the infinite Fibonacci sequence

In mathematics, the Fibonacci numbers, commonly denoted $F n$ , form a sequence, called the Fibonacci sequence, such that each number is the sum of the two preceding ones, starting from 0 and 1. That is,

In number theory, the Fermat pseudoprimes make up the most important class of pseudoprimes that come from Fermat's little theorem.

A palindromic number is a number that remains the same when its digits are reversed. In other words, it has reflectional symmetry across a vertical axis. The term palindromic is derived from palindrome, which refers to a word whose spelling is unchanged when its letters are reversed. The first 30 palindromic numbers are:

In recreational number theory, a unique prime or unique period prime is a certain kind of prime number. A prime p ≠ 2, 5 is called unique if there is no other prime q such that the period length of the decimal expansion of its reciprocal, 1 / p, is equal to the period length of the reciprocal of q, 1 / q. For example, 3 is the only prime with period 1, 11 is the only prime with period 2, 37 is the only prime with period 3, 101 is the only prime with period 4, so they are unique primes. In contrast, 41 and 271 both have period 5; 7 and 13 both have period 6; 239 and 4649 both have period 7; 73 and 137 both have period 8; 21649 and 513239 both have period 11; 53, 79 and 265371653 all have period 13; 31 and 2906161 both have period 15; 17 and 5882353 both have period 16; 2071723 and 5363222357 both have period 17; 19 and 52579 both have period 18; 3541 and 27961 both have period 20. Therefore, none of these is a unique prime. Unique primes were first described by Samuel Yates in 1980.

A power of two is a number of the form $2 n$ where $n$ is an integer, that is, the result of exponentiation with number two as the base and integer $n$ as the exponent.

In mathematics, and more particularly in number theory, primorial, denoted by “#”, is a function from natural numbers to natural numbers similar to the factorial function, but rather than successively multiplying positive integers, the function only multiplies prime numbers.

300 is the natural number following 299 and preceding 301.

500 is the natural number following 499 and preceding 501.

700 is the natural number following 699 and preceding 701.

The On-Line Encyclopedia of Integer Sequences (OEIS), also cited simply as Sloane's, is an online database of integer sequences. It was created and maintained by Neil Sloane while a researcher at AT&T Labs. He transferred the intellectual property and hosting of the OEIS to the OEIS Foundation in 2009. Sloane is president of the OEIS Foundation.

A pentagonal number is a figurate number that extends the concept of triangular and square numbers to the pentagon, but, unlike the first two, the patterns involved in the construction of pentagonal numbers are not rotationally symmetrical. The nth pentagonal number p_n is the number of distinct dots in a pattern of dots consisting of the outlines of regular pentagons with sides up to n dots, when the pentagons are overlaid so that they share one vertex. For instance, the third one is formed from outlines comprising 1, 5 and 10 dots, but the 1, and 3 of the 5, coincide with 3 of the 10 – leaving 12 distinct dots, 10 in the form of a pentagon, and 2 inside.

In number theory, a happy number is a number which eventually reaches 1 when replaced by the sum of the square of each digit. For instance, 13 is a happy number because $and . On the other hand, 4 is not a happy number because the sequence starting with and eventually reaches, the number that started the sequence, and so the process continues in an infinite cycle without ever reaching 1. A number which is not happy is called sad or unhappy .$

A pronic number is a number which is the product of two consecutive integers, that is, a number of the form $n (n + 1)$ . The study of these numbers dates back to Aristotle. They are also called oblong numbers, heteromecic numbers, or rectangular numbers; however, the term "rectangular number" has also been applied to the composite numbers.

In mathematics, the $n$ th Motzkin number is the number of different ways of drawing non-intersecting chords between $n$ points on a circle. The Motzkin numbers are named after Theodore Motzkin and have diverse applications in geometry, combinatorics and number theory.

The centered polygonal numbers are a class of series of figurate numbers, each formed by a central dot, surrounded by polygonal layers with a constant number of sides. Each side of a polygonal layer contains one dot more than a side in the previous layer, so starting from the second polygonal layer each layer of a centered k-gonal number contains k more points than the previous layer.

1,000,000,000 is the natural number following 999,999,999 and preceding 1,000,000,001. One billion can also be written as b or bn.

In number theory, a full reptend prime, full repetend prime, proper prime or long prime in base b is an odd prime number p such that the Fermat quotient

A Carol number is an integer of the form $or equivalently, The first few Carol numbers are: -1, 7, 47, 223, 959, 3967, 16127, 65023, 261119, 1046527.$

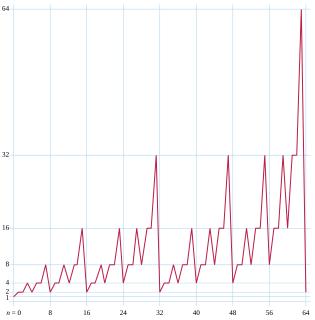
Gould's sequence is an integer sequence named after Henry W. Gould that counts the odd numbers in each row of Pascal's triangle. It consists only of powers of two, and begins:

References

↑ "Yahoo! Groups". groups.yahoo.com. Retrieved 2020-08-10.
↑ Entry for 852770th Kynea number at Prime Pages
↑ Carol and Kynea Prime Search by Mark Rodenkirch

External links

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] "Yahoo! Groups". groups.yahoo.com. Retrieved 2020-08-10.

[2] Entry for 852770th Kynea number at Prime Pages

[3] Carol and Kynea Prime Search by Mark Rodenkirch

Kynea numbers
n	Decimal	Binary
1	7	111
2	23	10111
3	79	1001111
4	287	100011111
5	1087	10000111111
6	4223	1000001111111
7	16639	100000011111111
8	66047	10000000111111111
9	263167	1000000001111111111

v t e Prime number classes
By formula	Fermat ( $2 2 n + 1$ ) Mersenne ( $2 p - 1$ ) Double Mersenne ( $2 2 p -1 - 1$ ) Wagstaff $(2 p + 1)/3$ Proth ( $k \cdot2 n + 1$ ) Factorial ( $n! \pm 1$ ) Primorial ( $p n # \pm 1$ ) Euclid ( $p n # + 1$ ) Pythagorean ( $4 n + 1$ ) Pierpont ( $2 m \cdot3 n + 1$ ) Quartan ( $x 4 + y 4$ ) Solinas ( $2 m \pm 2 n \pm 1$ ) Cullen ( $n \cdot2 n + 1$ ) Woodall ( $n \cdot2 n - 1$ ) Cuban ( $x 3 - y 3)/(x - y$ ) Carol $(2 n - 1) 2 - 2$ Kynea $(2 n + 1) 2 - 2$ Leyland ( $x y + y x$ ) Thabit ( $3\cdot2 n - 1$ ) Williams ( $(b -1)\cdot b n - 1$ ) Mills ( $⌊ A 3 n ⌋$ )
By integer sequence	Fibonacci Lucas Pell Newman–Shanks–Williams Perrin Partitions Bell Motzkin
By property	Wieferich (pair) Wall–Sun–Sun Wolstenholme Wilson Lucky Fortunate Ramanujan Pillai Regular Strong Stern Supersingular (elliptic curve) Supersingular (moonshine theory) Good Super Higgs Highly cototient
Base-dependent	Palindromic Emirp Repunit $(10 n - 1)/9$ Permutable Circular Truncatable Minimal Weakly Primeval Full reptend Unique Happy Self Smarandache–Wellin Strobogrammatic Dihedral Tetradic
Patterns	Twin ( $p, p + 2$ ) Bi-twin chain ( $n - 1, n + 1, 2 n - 1, 2 n + 1, \dots$ ) Triplet ( $p, p + 2 or p + 4, p + 6$ ) Quadruplet ( $p, p + 2, p + 6, p + 8$ ) k−Tuple Cousin ( $p, p + 4$ ) Sexy ( $p, p + 6$ ) Chen Sophie Germain/Safe ( $p, 2 p + 1$ ) Cunningham ( $p, 2 p \pm 1, 4 p \pm 3, 8 p \pm 7, ...$ ) Arithmetic progression ( $p + a\cdotn, n = 0, 1, 2, 3, ...$ ) Balanced ( $consecutive p - n, p, p + n$ )
By size	Titanic (1,000+ digits) Gigantic (10,000+ digits) Mega (1,000,000+ digits) Largest known
Complex numbers	Eisenstein prime Gaussian prime
Composite numbers	Pseudoprime Catalan Elliptic Euler Euler–Jacobi Fermat Frobenius Lucas Somer–Lucas Strong Carmichael number Almost prime Semiprime Interprime Pernicious
Related topics	Probable prime Industrial-grade prime Illegal prime Formula for primes Prime gap
First 60 primes	2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 101 103 107 109 113 127 131 137 139 149 151 157 163 167 173 179 181 191 193 197 199 211 223 227 229 233 239 241 251 257 263 269 271 277 281
List of prime numbers