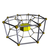
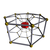
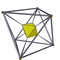
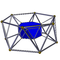
In geometry, a 4-polytope is a four-dimensional polytope. It is a connected and closed figure, composed of lower-dimensional polytopal elements: vertices, edges, faces (polygons), and cells (polyhedra). Each face is shared by exactly two cells.

In geometry, a prism is a polyhedron comprising an n-sided polygonal base, a second base which is a translated copy of the first, and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the bases are translations of the bases. Prisms are named for their bases, so a prism with a pentagonal base is called a pentagonal prism. The prisms are a subclass of the prismatoids.

In geometry, the Schläfli symbol is a notation of the form {p,q,r,...} that defines regular polytopes and tessellations.

In geometry, a uniform 4-polytope is a 4-dimensional polytope which is vertex-transitive and whose cells are uniform polyhedra, and faces are regular polygons.

In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher. The Cartesian product of an n-polytope and an m-polytope is an (n+m)-polytope, where n and m are 2 (polygon) or higher.

In four-dimensional geometry, a runcinated tesseract is a convex uniform 4-polytope, being a runcination of the regular tesseract.

The cubic honeycomb or cubic cellulation is the only proper regular space-filling tessellation in Euclidean 3-space, made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron. It is a self-dual tessellation with Schläfli symbol {4,3,4}. John Horton Conway calls this honeycomb a cubille.

In four-dimensional geometry, a runcinated 24-cell is a convex uniform 4-polytope, being a runcination of the regular 24-cell.

In geometry, a skew polygon is a polygon whose vertices are not all coplanar. Skew polygons must have at least 4 vertices. The interior surface of such a polygon is not uniquely defined.

A uniform polytope of dimension three or higher is a vertex-transitive polytope bounded by uniform facets. The uniform polytopes in two dimensions are the regular polygons.

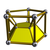
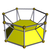
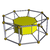
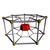
In 4-dimensional geometry, a uniform antiprismatic prism or antiduoprism is a uniform 4-polytope with two uniform antiprism cells in two parallel 3-space hyperplanes, connected by uniform prisms cells between pairs of faces. The symmetry of a p-gonal antiprismatic prism is [2p,2+,2], order 8p.

In geometry, a uniform 5-polytope is a five-dimensional uniform polytope. By definition, a uniform 5-polytope is vertex-transitive and constructed from uniform 4-polytope facets.

In the field of hyperbolic geometry, the order-4 hexagonal tiling honeycomb arises as one of 11 regular paracompact honeycombs in 3-dimensional hyperbolic space. It is called paracompact because it has infinite cells. Each cell consists of a hexagonal tiling whose vertices lie on a horosphere: a flat plane in hyperbolic space that approaches a single ideal point at infinity.

In geometry of 4 dimensions, a 8-8 duoprism or octagonal duoprism is a polygonal duoprism, a 4-polytope resulting from the Cartesian product of two octagons.

In geometry of 4 dimensions, a 6-6 duoprism or hexagonal duoprism is a polygonal duoprism, a 4-polytope resulting from the Cartesian product of two hexagons.

In geometry of 4 dimensions, a 4-6 duoprism, a duoprism and 4-polytope resulting from the Cartesian product of a square and a hexagon.

In geometry of 4 dimensions, a 4-8 duoprism, a duoprism and 4-polytope resulting from the Cartesian product of a square and an octagon.
In geometry of 4 dimensions, a 6-8 duoprism, a duoprism and 4-polytope resulting from the Cartesian product of a hexagon and an octagon.