Phase space formulation

Part of a series of articles about
Quantum mechanics
${\displaystyle i\hbar {\frac {\partial }{\partial t}}|\psi (t)\rangle ={\hat {H}}|\psi (t)\rangle }$ Schrödinger equation
Introduction Glossary History
Background Classical mechanics Old quantum theory Bra–ket notation Hamiltonian Interference
Fundamentals Casimir effect Coherence Decoherence Complementarity Energy level Entanglement Hamiltonian Uncertainty principle Ground state Interference Measurement Nonlocality Observable Operator Quantum Quantum fluctuation Quantum foam Quantum levitation Quantum number Quantum noise Quantum realm Quantum state Quantum system Quantum teleportation Qubit Spin Superposition Symmetry (Spontaneous) symmetry breaking Tunnelling Vacuum state Wave propagation Wave function Wave function collapse Wave–particle duality Matter wave
Experiments Afshar Bell's inequality Davisson–Germer Double-slit Elitzur–Vaidman Franck–Hertz Leggett–Garg inequality Mach–Zehnder Popper Quantum eraser  (delayed-choice) Schrödinger's cat Quantum suicide and immortality Stern–Gerlach Wheeler's delayed-choice
Formulations Overview Heisenberg Interaction Matrix Phase-space Schrödinger Sum-over-histories (path integral)
Equations Dirac Klein–Gordon Pauli Rydberg Schrödinger
Interpretations Overview Consistent histories Copenhagen de Broglie–Bohm Ensemble Hidden-variable Many-worlds Objective collapse Bayesian Quantum logic Relational Stochastic Scale relativity Transactional
Advanced topics Quantum annealing Quantum chaos Quantum computing Density matrix Quantum field theory Fractional quantum mechanics Quantum gravity Quantum information science Quantum machine learning Perturbation theory (quantum mechanics) Relativistic quantum mechanics Scattering theory Spontaneous parametric down-conversion Quantum statistical mechanics
Scientists Aharonov Bell Blackett Bloch Bohm Bohr Born Bose de Broglie Candlin Compton Dirac Davisson Debye Ehrenfest Einstein Everett Fock Fermi Feynman Glauber Gutzwiller Heisenberg Hilbert Jordan Kramers Pauli Lamb Landau Laue Moseley Millikan Onnes Planck Rabi Raman Rydberg Schrödinger Sommerfeld von Neumann Weyl Wien Wigner Zeeman Zeilinger
v t e

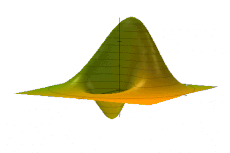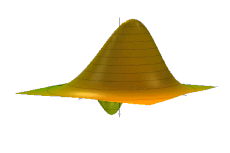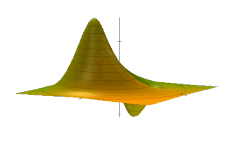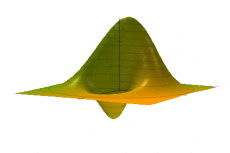
The phase space formulation of quantum mechanics places the position and momentum variables on equal footing, in phase space. In contrast, the Schrödinger picture uses the position or momentum representations (see also position and momentum space). The two key features of the phase space formulation are that the quantum state is described by a quasiprobability distribution (instead of a wave function, state vector, or density matrix) and operator multiplication is replaced by a star product .

The theory was fully developed by Hilbrand Groenewold in 1946 in his PhD thesis, ^[1] and independently by Joe Moyal, ^[2] each building on earlier ideas by Hermann Weyl ^[3] and Eugene Wigner. ^[4]

The chief advantage of the phase space formulation is that it makes quantum mechanics appear as similar to Hamiltonian mechanics as possible by avoiding the operator formalism, thereby "'freeing' the quantization of the 'burden' of the Hilbert space". ^[5] This formulation is statistical in nature and offers logical connections between quantum mechanics and classical statistical mechanics, enabling a natural comparison between the two (cf. classical limit). Quantum mechanics in phase space is often favored in certain quantum optics applications (see optical phase space), or in the study of decoherence and a range of specialized technical problems, though otherwise the formalism is less commonly employed in practical situations. ^[6]

The conceptual ideas underlying the development of quantum mechanics in phase space have branched into mathematical offshoots such as algebraic deformation theory (cf. Kontsevich quantization formula) and noncommutative geometry.

Phase space distribution

Main articles: Wigner quasiprobability distribution, Quasiprobability distribution, and Wigner–Weyl transform

The phase space distribution f(x,p) of a quantum state is a quasiprobability distribution. In the phase space formulation, the phase-space distribution may be treated as the fundamental, primitive description of the quantum system, without any reference to wave functions or density matrices. ^[7]

There are several different ways to represent the distribution, all interrelated. ^{[8] [9]} The most noteworthy is the Wigner representation, W(x,p), discovered first. ^[4] Other representations (in approximately descending order of prevalence in the literature) include the Glauber-Sudarshan P, ^{[10] [11]} Husimi Q, ^[12] Kirkwood-Rihaczek, Mehta, Rivier, and Born-Jordan representations. ^{[13] [14]} These alternatives are most useful when the Hamiltonian takes a particular form, such as normal order for the Glauber–Sudarshan P-representation. Since the Wigner representation is the most common, this article will usually stick to it, unless otherwise specified.

The phase space distribution possesses properties akin to the probability density in a 2n-dimensional phase space. For example, it is real-valued, unlike the generally complex-valued wave function. We can understand the probability of lying within a position interval, for example, by integrating the Wigner function over all momenta and over the position interval:

${\displaystyle \operatorname {P} [a\leq X\leq b]=\int _{a}^{b}\int _{-\infty }^{\infty }W(x,p)\,dp\,dx.}$

If Â(x,p) is an operator representing an observable, it may be mapped to phase space as A(x, p) through the Wigner transform . Conversely, this operator may be recovered via the Weyl transform .

The expectation value of the observable with respect to the phase space distribution is ^{[2] [15]}

${\displaystyle \langle {\hat {A}}\rangle =\int A(x,p)W(x,p)\,dp\,dx.}$

A point of caution, however: despite the similarity in appearance, W(x,p) is not a genuine joint probability distribution, because regions under it do not represent mutually exclusive states, as required in the third axiom of probability theory. Moreover, it can, in general, take negative values even for pure states, with the unique exception of (optionally squeezed) coherent states, in violation of the first axiom.

Regions of such negative value are provable to be "small": they cannot extend to compact regions larger than a few ħ, and hence disappear in the classical limit. They are shielded by the uncertainty principle, which does not allow precise localization within phase-space regions smaller than ħ, and thus renders such "negative probabilities" less paradoxical. If the left side of the equation is to be interpreted as an expectation value in the Hilbert space with respect to an operator, then in the context of quantum optics this equation is known as the optical equivalence theorem. (For details on the properties and interpretation of the Wigner function, see its main article.)

An alternative phase space approach to quantum mechanics seeks to define a wave function (not just a quasiprobability density) on phase space, typically by means of the Segal–Bargmann transform. To be compatible with the uncertainty principle, the phase space wave function cannot be an arbitrary function, or else it could be localized into an arbitrarily small region of phase space. Rather, the Segal–Bargmann transform is a holomorphic function of ${\displaystyle x+ip}$. There is a quasiprobability density associated to the phase space wave function; it is the Husimi Q representation of the position wave function.

Star product

Main article: Moyal product

The fundamental noncommutative binary operator in the phase space formulation that replaces the standard operator multiplication is the star product, represented by the symbol ★. ^[1] Each representation of the phase-space distribution has a different characteristic star product. For concreteness, we restrict this discussion to the star product relevant to the Wigner-Weyl representation.

For notational convenience, we introduce the notion of left and right derivatives. For a pair of functions f and g, the left and right derivatives are defined as

${\displaystyle f{\overleftarrow {\partial }}_{x}g={\frac {\partial f}{\partial x}}\cdot g}$

${\displaystyle f{\overrightarrow {\partial }}_{x}g=f\cdot {\frac {\partial g}{\partial x}}.}$

The differential definition of the star product is

${\displaystyle f\star g=f\,\exp {\left({\tfrac {i\hbar }{2}}({\overleftarrow {\partial }}_{x}{\overrightarrow {\partial }}_{p}-{\overleftarrow {\partial }}_{p}{\overrightarrow {\partial }}_{x})\right)}\,g}$

where the argument of the exponential function can be interpreted as a power series. Additional differential relations allow this to be written in terms of a change in the arguments of f and g:

${\displaystyle {\begin{aligned}(f\star g)(x,p)&=f\left(x+{\tfrac {i\hbar }{2}}{\overrightarrow {\partial }}_{p},p-{\tfrac {i\hbar }{2}}{\overrightarrow {\partial }}_{x}\right)\cdot g(x,p)\\&=f(x,p)\cdot g\left(x-{\tfrac {i\hbar }{2}}{\overleftarrow {\partial }}_{p},p+{\tfrac {i\hbar }{2}}{\overleftarrow {\partial }}_{x}\right)\\&=f\left(x+{\tfrac {i\hbar }{2}}{\overrightarrow {\partial }}_{p},p\right)\cdot g\left(x-{\tfrac {i\hbar }{2}}{\overleftarrow {\partial }}_{p},p\right)\\&=f\left(x,p-{\tfrac {i\hbar }{2}}{\overrightarrow {\partial }}_{x}\right)\cdot g\left(x,p+{\tfrac {i\hbar }{2}}{\overleftarrow {\partial }}_{x}\right).\end{aligned}}}$

It is also possible to define the ★-product in a convolution integral form, ^[16] essentially through the Fourier transform:

${\displaystyle (f\star g)(x,p)={\frac {1}{\pi ^{2}\hbar ^{2}}}\,\int f(x+x',p+p')\,g(x+x'',p+p'')\,\exp {\left({\tfrac {2i}{\hbar }}(x'p''-x''p')\right)}\,dx'dp'dx''dp''~.}$

(Thus, e.g., ^[7] Gaussians compose hyperbolically,

${\displaystyle \exp \left(-{a}(x^{2}+p^{2})\right)~\star ~\exp \left(-{b}(x^{2}+p^{2})\right)={1 \over 1+\hbar ^{2}ab}\exp \left(-{a+b \over 1+\hbar ^{2}ab}(x^{2}+p^{2})\right),}$

or

${\displaystyle \delta (x)~\star ~\delta (p)={2 \over h}\exp \left(2i{xp \over \hbar }\right),}$

etc.)

The energy eigenstate distributions are known as stargenstates, ★-genstates, stargenfunctions, or ★-genfunctions, and the associated energies are known as stargenvalues or ★-genvalues. These are solved fin, analogously to the time-independent Schrödinger equation, by the ★-genvalue equation, ^{[17] [18]}

${\displaystyle H\star W=E\cdot W,}$

where H is the Hamiltonian, a plain phase-space function, most often identical to the classical Hamiltonian.

Time evolution

The time evolution of the phase space distribution is given by a quantum modification of Liouville flow. ^{[2] [9] [19]} This formula results from applying the Wigner transformation to the density matrix version of the quantum Liouville equation, the von Neumann equation.

In any representation of the phase space distribution with its associated star product, this is

${\displaystyle {\frac {\partial f}{\partial t}}=-{\frac {1}{i\hbar }}\left(f\star H-H\star f\right),}$

or, for the Wigner function in particular,

${\displaystyle {\frac {\partial W}{\partial t}}=-\{\{W,H\}\}=-{\frac {2}{\hbar }}W\sin \left({{\frac {\hbar }{2}}({\overset {\leftarrow }{\partial _{x}}}{\overset {\rightarrow }{\partial _{p}}}-{\overset {\leftarrow }{\partial _{p}}}{\overset {\rightarrow }{\partial _{x}}})}\right)\ H=-\{W,H\}+O(\hbar ^{2}),}$

where {{ , }} is the Moyal bracket, the Wigner transform of the quantum commutator, while { , } is the classical Poisson bracket. ^[2]

This yields a concise illustration of the correspondence principle: this equation manifestly reduces to the classical Liouville equation in the limit ħ → 0. In the quantum extension of the flow, however, the density of points in phase space is not conserved; the probability fluid appears "diffusive" and compressible. ^[2] The concept of quantum trajectory is therefore a delicate issue here. (Given the restrictions placed by the uncertainty principle on localization, Niels Bohr vigorously denied the physical existence of such trajectories on the microscopic scale. By means of formal phase-space trajectories, the time evolution problem of the Wigner function can be rigorously solved using the path-integral method ^[20] and the method of quantum characteristics, ^[21] although there are unforgiving practical obstacles in both cases.) See the movie for the Morse potential, below, to appreciate the rapid diffusion of would-be trajectories.

Examples

Simple harmonic oscillator

Main article: quantum harmonic oscillator

The Wigner quasiprobability distribution F_n(u) for the simple harmonic oscillator with a) n = 0, b) n = 1, and c) n = 5.

The Hamiltonian for the simple harmonic oscillator in one spatial dimension in the Wigner-Weyl representation is

${\displaystyle H={\frac {1}{2}}m\omega ^{2}x^{2}+{\frac {p^{2}}{2m}}.}$

The ★-genvalue equation for the static Wigner function then reads

${\displaystyle {\begin{aligned}H\star W&=\left({\frac {1}{2}}m\omega ^{2}x^{2}+{\frac {p^{2}}{2m}}\right)\star W\\&=\left({\frac {1}{2}}m\omega ^{2}\left(x+{\frac {i\hbar }{2}}{\stackrel {\rightarrow }{\partial }}_{p}\right)^{2}+{\frac {1}{2m}}\left(p-{\frac {i\hbar }{2}}{\stackrel {\rightarrow }{\partial }}_{x}\right)^{2}\right)~W\\&=\left({\frac {1}{2}}m\omega ^{2}\left(x^{2}-{\frac {\hbar ^{2}}{4}}{\stackrel {\rightarrow }{\partial }}_{p}^{2}\right)+{\frac {1}{2m}}\left(p^{2}-{\frac {\hbar ^{2}}{4}}{\stackrel {\rightarrow }{\partial }}_{x}^{2}\right)\right)~W\\&\,\,\,\,\,+{\frac {i\hbar }{2}}\left(m\omega ^{2}x{\stackrel {\rightarrow }{\partial }}_{p}-{\frac {p}{m}}{\stackrel {\rightarrow }{\partial }}_{x}\right)~W\\&=E\cdot W.\end{aligned}}}$

Time evolution of combined ground and 1st excited state Wigner function for the simple harmonic oscillator. Note the rigid motion in phase space corresponding to the conventional oscillations in coordinate space.

Wigner function for the harmonic oscillator ground state, displaced from the origin of phase space, i.e., a coherent state. Note the rigid rotation, identical to classical motion: this is a special feature of the SHO, illustrating the correspondence principle. From the general pedagogy web-site. ^[22]

(Click to animate.)

Consider first the imaginary part of the ★-genvalue equation.

${\displaystyle {\frac {\hbar }{2}}\left(m\omega ^{2}x{\overrightarrow {\partial }}_{p}-{\frac {p}{m}}{\overrightarrow {\partial }}_{x}\right)\cdot W=0}$

This implies that one may write the ★-genstates as functions of a single argument,

${\displaystyle W(x,p)=F\left({\frac {1}{2}}m\omega ^{2}x^{2}+{\frac {p^{2}}{2m}}\right)\equiv F(u).}$

With this change of variables, it is possible to write the real part of the ★-genvalue equation in the form of a modified Laguerre equation (not Hermite's equation!), the solution of which involves the Laguerre polynomials as ^[18]

${\displaystyle F_{n}(u)={\frac {(-1)^{n}}{\pi \hbar }}L_{n}\left(4{\frac {u}{\hbar \omega }}\right)e^{-2u/\hbar \omega }~,}$

introduced by Groenewold in his paper, ^[1] with associated ★-genvalues

${\displaystyle E_{n}=\hbar \omega \left(n+{\frac {1}{2}}\right)~.}$

For the harmonic oscillator, the time evolution of an arbitrary Wigner distribution is simple. An initial W(x,p; t=0) = F(u) evolves by the above evolution equation driven by the oscillator Hamiltonian given, by simply rigidly rotating in phase space, ^[1]

${\displaystyle W(x,p;t)=W(m\omega x\cos \omega t-p\sin \omega t,~p\cos \omega t+\omega mx\sin \omega t;0)~.}$

Typically, a "bump" (or coherent state) of energy E ≫ ħω can represent a macroscopic quantity and appear like a classical object rotating uniformly in phase space, a plain mechanical oscillator (see the animated figures). Integrating over all phases (starting positions at t = 0) of such objects, a continuous "palisade", yields a time-independent configuration similar to the above static ★-genstates F(u), an intuitive visualization of the classical limit for large action systems. ^[6]

Free particle angular momentum

Suppose a particle is initially in a minimally uncertain Gaussian state, with the expectation values of position and momentum both centered at the origin in phase space. The Wigner function for such a state propagating freely is

${\displaystyle W(\mathbf {x} ,\mathbf {p} ;t)={\frac {1}{(\pi \hbar )^{3}}}\exp {\left(-\alpha ^{2}r^{2}-{\frac {p^{2}}{\alpha ^{2}\hbar ^{2}}}\left(1+\left({\frac {t}{\tau }}\right)^{2}\right)+{\frac {2t}{\hbar \tau }}\mathbf {x} \cdot \mathbf {p} \right)}~,}$

where α is a parameter describing the initial width of the Gaussian, and τ = m/α²ħ.

Initially, the position and momenta are uncorrelated. Thus, in 3 dimensions, we expect the position and momentum vectors to be twice as likely to be perpendicular to each other as parallel.

However, the position and momentum become increasingly correlated as the state evolves, because portions of the distribution farther from the origin in position require a larger momentum to be reached: asymptotically,

${\displaystyle W\longrightarrow {\frac {1}{(\pi \hbar )^{3}}}\exp \left[-\alpha ^{2}\left(\mathbf {x} -{\frac {\mathbf {p} t}{m}}\right)^{2}\right]\,.}$

(This relative "squeezing" reflects the spreading of the free wave packet in coordinate space.)

Indeed, it is possible to show that the kinetic energy of the particle becomes asymptotically radial only, in agreement with the standard quantum-mechanical notion of the ground-state nonzero angular momentum specifying orientation independence: ^[23]

${\displaystyle K_{rad}={\frac {\alpha ^{2}\hbar ^{2}}{2m}}\left({\frac {3}{2}}-{\frac {1}{1+(t/\tau )^{2}}}\right)}$

${\displaystyle K_{ang}={\frac {\alpha ^{2}\hbar ^{2}}{2m}}{\frac {1}{1+(t/\tau )^{2}}}~.}$

Morse potential

The Morse potential is used to approximate the vibrational structure of a diatomic molecule.

The Wigner function time-evolution of the Morse potential U(x) = 20(1 − e^−0.16x)² in atomic units (a.u.). The solid lines represent level set of the Hamiltonian H(x, p) = p²/2 + U(x).

Quantum tunneling

Tunneling is a hallmark quantum effect where a quantum particle, not having sufficient energy to fly above, still goes through a barrier. This effect does not exist in classical mechanics.

The Wigner function for tunneling through the potential barrier U(x) = 8e^−0.25x2 in atomic units (a.u.). The solid lines represent the level set of the Hamiltonian H(x, p) = p²/2 + U(x).

Quartic potential

The Wigner function time evolution for the potential U(x) = 0.1x⁴ in atomic units (a.u.). The solid lines represent the level set of the Hamiltonian H(x, p) = p²/2 + U(x).

Schrödinger cat state

Wigner function of two interfering coherent states evolving through the SHO Hamiltonian. The corresponding momentum and coordinate projections are plotted to the right and under the phase space plot.

References

1. H.J. Groenewold, "On the Principles of elementary quantum mechanics", Physica,12 (1946) pp. 405–460. doi : 10.1016/S0031-8914(46)80059-4
2. J.E. Moyal, "Quantum mechanics as a statistical theory", Proceedings of the Cambridge Philosophical Society, 45 (1949) pp. 99–124. doi : 10.1017/S0305004100000487
3. H.Weyl, "Quantenmechanik und Gruppentheorie", Zeitschrift für Physik, 46 (1927) pp. 1–46, doi : 10.1007/BF02055756
4. E.P. Wigner, "On the quantum correction for thermodynamic equilibrium", Phys. Rev.40 (June 1932) 749–759. doi : 10.1103/PhysRev.40.749
5. S. T. Ali, M. Engliš, "Quantization Methods: A Guide for Physicists and Analysts." Rev.Math.Phys., 17 (2005) pp. 391-490. doi : 10.1142/S0129055X05002376
6. Curtright, T. L.; Zachos, C. K. (2012). "Quantum Mechanics in Phase Space". Asia Pacific Physics Newsletter. 01: 37. arXiv: 1104.5269  . doi:10.1142/S2251158X12000069. 
7. C. Zachos, D. Fairlie, and T. Curtright, "Quantum Mechanics in Phase Space" ( World Scientific, Singapore, 2005) ISBN   978-981-238-384-6.
8. Cohen, L. (1966). "Generalized Phase-Space Distribution Functions". Journal of Mathematical Physics. 7 (5): 781–781. Bibcode:1966JMP.....7..781C. doi:10.1063/1.1931206. 
9. G. S. Agarwal and E. Wolf "Calculus for Functions of Noncommuting Operators and General Phase-Space Methods in Quantum Mechanics. II. Quantum Mechanics in Phase Space", Phys. Rev. D,2 (1970) pp. 2187–2205. doi : 10.1103/PhysRevD.2.2187
10. E. C. G. Sudarshan "Equivalence of Semiclassical and Quantum Mechanical Descriptions of Statistical Light Beams", Phys. Rev. Lett.,10 (1963) pp. 277–279. doi : 10.1103/PhysRevLett.10.277
11. R. J. Glauber "Coherent and Incoherent States of the Radiation Field", Phys. Rev.,131 (1963) pp. 2766–2788. doi : 10.1103/PhysRev.131.2766
12. Kôdi Husimi (1940). "Some Formal Properties of the Density Matrix", Proc. Phys. Math. Soc. Jpn.22: 264-314 .
13. G. S. Agarwal and E. Wolf "Calculus for Functions of Noncommuting Operators and General Phase-Space Methods in Quantum Mechanics. I. Mapping Theorems and Ordering of Functions of Noncommuting Operators", Phys. Rev. D,2 (1970) pp. 2161–2186. doi : 10.1103/PhysRevD.2.2161
14. K. E. Cahill and R. J. Glauber "Ordered Expansions in Boson Amplitude Operators", Phys. Rev.,177 (1969) pp. 1857–1881. doi : 10.1103/PhysRev.177.1857; K. E. Cahill and R. J. Glauber "Density Operators and Quasiprobability Distributions", Phys. Rev.,177 (1969) pp. 1882–1902. doi : 10.1103/PhysRev.177.1882
15. M. Lax "Quantum Noise. XI. Multitime Correspondence between Quantum and Classical Stochastic Processes", Phys. Rev.,172 (1968) pp. 350–361. doi : 10.1103/PhysRev.172.350
16. G. Baker, “Formulation of Quantum Mechanics Based on the Quasi-probability Distribution Induced on Phase Space,” Physical Review, 109 (1958) pp.2198–2206. doi : 10.1103/PhysRev.109.2198
17. Fairlie, D. B. (1964). "The formulation of quantum mechanics in terms of phase space functions". Mathematical Proceedings of the Cambridge Philosophical Society. 60 (3): 581. Bibcode:1964PCPS...60..581F. doi:10.1017/S0305004100038068. 
18. Curtright, T.; Fairlie, D.; Zachos, C. (1998). "Features of time-independent Wigner functions". Physical Review D. 58 (2). arXiv: hep-th/9711183  . Bibcode:1998PhRvD..58b5002C. doi:10.1103/PhysRevD.58.025002. 
19. C. L. Mehta "Phase‐Space Formulation of the Dynamics of Canonical Variables", J. Math. Phys.,5 (1964) pp. 677–686. doi : 10.1063/1.1704163
20. M. S. Marinov, A new type of phase-space path integral, Phys. Lett. A 153, 5 (1991).
21. M. I. Krivoruchenko, A. Faessler, Weyl's symbols of Heisenberg operators of canonical coordinates and momenta as quantum characteristics, J. Math. Phys. 48, 052107 (2007) doi : 10.1063/1.2735816.
22. Curtright, T.L. Time-dependent Wigner Functions
23. J. P. Dahl and W. P. Schleich, "Concepts of radial and angular kinetic energies", Phys. Rev. A,65 (2002). doi : 10.1103/PhysRevA.65.022109