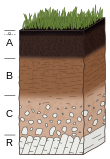
The water table is the upper surface of the zone of saturation. The zone of saturation is where the pores and fractures of the ground are saturated with groundwater, which may be fresh, saline, or brackish, depending on the locality. It can also be simply explained as the depth below which the ground is saturated.
Water potential is the potential energy of water per unit volume relative to pure water in reference conditions. Water potential quantifies the tendency of water to move from one area to another due to osmosis, gravity, mechanical pressure and matrix effects such as capillary action. The concept of water potential has proved useful in understanding and computing water movement within plants, animals, and soil. Water potential is typically expressed in potential energy per unit volume and very often is represented by the Greek letter ψ.

Soil mechanics is a branch of soil physics and applied mechanics that describes the behavior of soils. It differs from fluid mechanics and solid mechanics in the sense that soils consist of a heterogeneous mixture of fluids and particles but soil may also contain organic solids and other matter. Along with rock mechanics, soil mechanics provides the theoretical basis for analysis in geotechnical engineering, a subdiscipline of civil engineering, and engineering geology, a subdiscipline of geology. Soil mechanics is used to analyze the deformations of and flow of fluids within natural and man-made structures that are supported on or made of soil, or structures that are buried in soils. Example applications are building and bridge foundations, retaining walls, dams, and buried pipeline systems. Principles of soil mechanics are also used in related disciplines such as geophysical engineering, coastal engineering, agricultural engineering, and hydrology.

Soil moisture is the water content of the soil. It can be expressed in terms of volume or weight. Soil moisture measurement can be based on in situ probes or remote sensing methods.

The vadose zone, also termed the unsaturated zone, is the part of Earth between the land surface and the top of the phreatic zone, the position at which the groundwater is at atmospheric pressure. Hence, the vadose zone extends from the top of the ground surface to the water table.

Water content or moisture content is the quantity of water contained in a material, such as soil, rock, ceramics, crops, or wood. Water content is used in a wide range of scientific and technical areas, and is expressed as a ratio, which can range from 0 to the value of the materials' porosity at saturation. It can be given on a volumetric or mass (gravimetric) basis.
Soil physics is the study of soil's physical properties and processes. It is applied to management and prediction under natural and managed ecosystems. Soil physics deals with the dynamics of physical soil components and their phases as solids, liquids, and gases. It draws on the principles of physics, physical chemistry, engineering, and meteorology. Soil physics applies these principles to address practical problems of agriculture, ecology, and engineering.

The capillary fringe is the subsurface layer in which groundwater seeps up from a water table by capillary action to fill pores. Pores at the base of the capillary fringe are filled with water due to tension saturation. This saturated portion of the capillary fringe is less than the total capillary rise because of the presence of a mix in pore size. If the pore size is small and relatively uniform, it is possible that soils can be completely saturated with water for several feet above the water table. Alternately, when the pore size is large, the saturated portion will extend only a few inches above the water table. Capillary action supports a vadose zone above the saturated base, within which water content decreases with distance above the water table. In soils with a wide range in pore size, the unsaturated zone can be several times thicker than the saturated zone.

Infiltration is the process by which water on the ground surface enters the soil. It is commonly used in both hydrology and soil sciences. The infiltration capacity is defined as the maximum rate of infiltration. It is most often measured in meters per day but can also be measured in other units of distance over time if necessary. The infiltration capacity decreases as the soil moisture content of soils surface layers increases. If the precipitation rate exceeds the infiltration rate, runoff will usually occur unless there is some physical barrier.
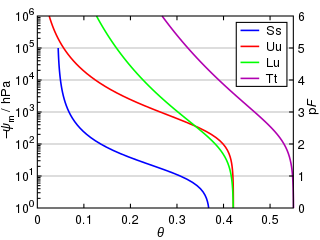
Water retention curve is the relationship between the water content, θ, and the soil water potential, ψ. The soil moisture curve is characteristic for different types of soil, and is also called the soil moisture characteristic.

The effective stress can be defined as the stress, depending on the applied tension and pore pressure , which controls the strain or strength behaviour of soil and rock for whatever pore pressure value or, in other terms, the stress which applied over a dry porous body provides the same strain or strength behaviour which is observed at ≠ 0. In the case of granular media it can be viewed as a force that keeps a collection of particles rigid. Usually this applies to sand, soil, or gravel, as well as every kind of rock and several other porous materials such as concrete, metal powders, biological tissues etc. The usefulness of an appropriate ESP formulation consists in allowing to assess the behaviour of a porous body for whatever pore pressure value on the basis of experiments involving dry samples.
The void ratio of a mixture of solids and fluids, or of a porous composite material such as concrete, is the ratio of the volume of the voids filled by the fluids to the volume of all the solids. It is a dimensionless quantity in materials science and in soil science, and is closely related to the porosity, the ratio of the volume of voids to the total volume, as follows:
The pore space of soil contains the liquid and gas phases of soil, i.e., everything but the solid phase that contains mainly minerals of varying sizes as well as organic compounds.

The phreatic zone, saturated zone, or zone of saturation, is the part of an aquifer, below the water table, in which relatively all pores and fractures are saturated with water. The part above the water table is the vadose zone.

Minerals bond grains of sediment together by growing around them. This process is called cementation and is a part of the rock cycle.
Porosity or void fraction is a measure of the void spaces in a material, and is a fraction of the volume of voids over the total volume, between 0 and 1, or as a percentage between 0% and 100%. Strictly speaking, some tests measure the "accessible void", the total amount of void space accessible from the surface.
Preconsolidation pressure is the maximum effective vertical overburden stress that a particular soil sample has sustained in the past. This quantity is important in geotechnical engineering, particularly for finding the expected settlement of foundations and embankments. Alternative names for the preconsolidation pressure are preconsolidation stress, pre-compression stress, pre-compaction stress, and preload stress. A soil is called overconsolidated if the current effective stress acting on the soil is less than the historical maximum.

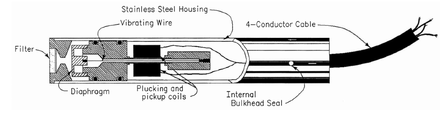
A tensiometer in soil science is a measuring instrument used to determine the matric water potential in the vadose zone. This device typically consists of a glass or plastic tube with a porous ceramic cup and is filled with water. The top of the tube has either a built-in vacuum gauge or a rubber cap used with a portable puncture tensiometer instrument, which uses a hypodermic needle to measure the pressure inside the tensiometer. The tensiometer is buried in the soil, and a hand pump is used to pull a partial vacuum. As water is pulled out of the soil by plants and evaporation, the vacuum inside the tube increases. When the soil is wetted flow can also occur in the reverse direction: as water is added to the soil, the vacuum inside the tube pulls moisture from the soil and decreases. When the water pressure in the tensiometer is determined to be in equilibrium with the water pressure in the soil, the tensiometer gauge reading represents the matric potential of the soil.

The finite water-content vadose zone flux method represents a one-dimensional alternative to the numerical solution of Richards' equation for simulating the movement of water in unsaturated soils. The finite water-content method solves the advection-like term of the Soil Moisture Velocity Equation, which is an ordinary differential equation alternative to the Richards partial differential equation. The Richards equation is difficult to approximate in general because it does not have a closed-form analytical solution except in a few cases. The finite water-content method, is perhaps the first generic replacement for the numerical solution of the Richards' equation. The finite water-content solution has several advantages over the Richards equation solution. First, as an ordinary differential equation it is explicit, guaranteed to converge and computationally inexpensive to solve. Second, using a finite volume solution methodology it is guaranteed to conserve mass. The finite water content method readily simulates sharp wetting fronts, something that the Richards solution struggles with. The main limiting assumption required to use the finite water-content method is that the soil be homogeneous in layers.
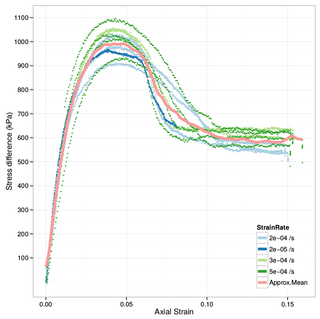
In soil mechanics, dilatancy or shear dilatancy is the volume change observed in granular materials when they are subjected to shear deformations. This effect was first described scientifically by Osborne Reynolds in 1885/1886 and is also known as Reynolds dilatancy. It was brought into the field of geotechnical engineering by Peter Walter Rowe.