In technology, Chiplets are tiny hardware subsystem implementations of SoCs (systems on a chip) which can be interconnected into larger, or more responsive surroundings. Packaging SoCs into small hardware multi-chip packages allows more effective functions which confer a competitive advantage in economics, wars, or politics.[26]
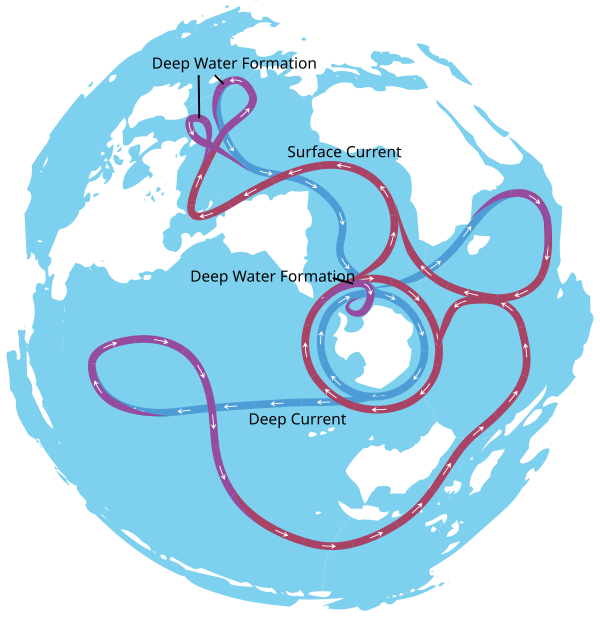
The thermohaline circulation can occur from the deep oceans to the ocean's surface. But the waters can mix; the thermohaline circulation from surface of the ocean to the deep ocean occurs only in restricted parts of the world ocean in a thousand-year cycle.
1 2 3 The theme of the issue on Varieties of abstract concepts (18 June 2018) is "grounded in sensorimotor systems, linguistic, emotional, and social experiences".[1] Section 3a of the 5 Aug 2018 issue is "grounding of abstract concepts in multiple systems" (such as sociality, linguistics, perceptionaction, interoception, and metacognitionSee figure 1).[1]
↑ Geoffrey Hodgson calls institutions "integrated systems of rules that structure social interactions".[2]
↑ Earth and Moon form a binary system whose barycenter lies within Earth itself. The effect on Earth's trajectory is observed as a "wobble" of an otherwise elliptical orbit of Earth around the Sun.
↑ Large language models (LLMs) are allowing mathematicians to revisit mathematical proofs which they have already written. These LLMs are mechanical 'proof whiners'; the LLMs provide line-by-line feedback to the mathematicians, which highlight the parts of the proof which the mathematicians need to rewrite so that the proof assistants can get past roadblocks.[23] This deep introspection allows the mathematicians deeper insight into their proofs.[23][24]
↑ Meadows (2008)[9][10] noted that systems could be resilient, and surprising. They can display §emergent abilities which can confer a relative advantage, temporarily. Terence Tao noted that it helps when the robots are cute and non-threatening.[24]
Abstraction is a process wherein general rules and concepts are derived from the usage and classification of specific examples, literal signifiers, first principles, or other methods.
A concept is defined as an abstract idea. It is understood to be a fundamental building block underlying principles, thoughts and beliefs. Concepts play an important role in all aspects of cognition. As such, concepts are studied within such disciplines as linguistics, psychology, and philosophy, and these disciplines are interested in the logical and psychological structure of concepts, and how they are put together to form thoughts and sentences. The study of concepts has served as an important flagship of an emerging interdisciplinary approach, cognitive science.
In logic, mathematics, computer science, and linguistics, a formal language consists of words whose letters are taken from an alphabet and are well-formed according to a specific set of rules called a formal grammar.
Where Mathematics Comes From: How the Embodied Mind Brings Mathematics into Being is a book by George Lakoff, a cognitive linguist, and Rafael E. Núñez, a psychologist. Published in 2000, WMCF seeks to found a cognitive science of mathematics, a theory of embodied mathematics based on conceptual metaphor.
The philosophy of mathematics is the branch of philosophy that studies the assumptions, foundations, and implications of mathematics. It aims to understand the nature and methods of mathematics, and find out the place of mathematics in people's lives.
Reductionism is any of several related philosophical ideas regarding the associations between phenomena which can be described in terms of other simpler or more fundamental phenomena. It is also described as an intellectual and philosophical position that interprets a complex system as the sum of its parts.
In cognitive linguistics, conceptual metaphor, or cognitive metaphor, refers to the understanding of one idea, or conceptual domain, in terms of another. An example of this is the understanding of quantity in terms of directionality or the understanding of time in terms of money.
Pragmatism is a philosophical tradition that views language and thought as tools for prediction, problem solving, and action, rather than describing, representing, or mirroring reality. Pragmatists contend that most philosophical topics—such as the nature of knowledge, language, concepts, meaning, belief, and science—are all best viewed in terms of their practical uses and successes.
Sentience is the simplest or most primitive form of cognition, consisting of a conscious awareness of stimuli without association or interpretation. The word was first coined by philosophers in the 1630s for the concept of an ability to feel, derived from Latin sentiens (feeling), to distinguish it from the ability to think (reason).
Foundations of mathematics is the study of the philosophical and logical and/or algorithmic basis of mathematics, or, in a broader sense, the mathematical investigation of what underlies the philosophical theories concerning the nature of mathematics. In this latter sense, the distinction between foundations of mathematics and philosophy of mathematics turns out to be vague. Foundations of mathematics can be conceived as the study of the basic mathematical concepts and how they form hierarchies of more complex structures and concepts, especially the fundamentally important structures that form the language of mathematics also called metamathematical concepts, with an eye to the philosophical aspects and the unity of mathematics. The search for foundations of mathematics is a central question of the philosophy of mathematics; the abstract nature of mathematical objects presents special philosophical challenges.
Thomas Nagel is an American philosopher. He is the University Professor of Philosophy and Law Emeritus at New York University, where he taught from 1980 to 2016. His main areas of philosophical interest are legal philosophy, political philosophy, and ethics.
Systems thinking is a way of making sense of the complexity of the world by looking at it in terms of wholes and relationships rather than by splitting it down into its parts. It has been used as a way of exploring and developing effective action in complex contexts, enabling systems change. Systems thinking draws on and contributes to systems theory and the system sciences.
The Society of Mind is both the title of a 1986 book and the name of a theory of natural intelligence as written and developed by Marvin Minsky.
Eugene Tovio Gendlin was an American philosopher who developed ways of thinking about and working with living process, the bodily felt sense and the "philosophy of the implicit". Though he had no degree in the field of psychology, his advanced study with Carl Rogers, his longtime practice of psychotherapy and his extensive writings in the field of psychology have made him perhaps better known in that field than in philosophy. He studied under Carl Rogers, the founder of client-centered therapy, at the University of Chicago and received his PhD in philosophy in 1958. Gendlin's theories impacted Rogers' own beliefs and played a role in Rogers' view of psychotherapy. From 1958 to 1963 Gendlin was Research Director at the Wisconsin Psychiatric Institute of the University of Wisconsin. He served as an associate professor in the departments of Philosophy and Comparative Human Development at the University of Chicago from 1964 until 1995.
Vyākaraṇa refers to one of the six ancient Vedangas, ancillary science connected with the Vedas, which are scriptures in Hinduism. Vyākaraṇa is the study of grammar and linguistic analysis in Sanskrit language.
Pāṇini was a logician, Sanskrit philologist, grammarian, and revered scholar in ancient India, variously dated between the 6th and 4th century BCE.
High-level and low-level, as technical terms, are used to classify, describe and point to specific goals of a systematic operation; and are applied in a wide range of contexts, such as, for instance, in domains as widely varied as computer science and business administration.
The following outline is provided as an overview of and topical guide to thought (thinking):
The Aṣṭādhyāyī is a grammar that describes a form of an early Indo-Aryan language: Sanskrit.
In the philosophy of mathematics, formalism is the view that holds that statements of mathematics and logic can be considered to be statements about the consequences of the manipulation of strings using established manipulation rules. A central idea of formalism "is that mathematics is not a body of propositions representing an abstract sector of reality, but is much more akin to a game, bringing with it no more commitment to an ontology of objects or properties than ludo or chess." According to formalism, the truths expressed in logic and mathematics are not about numbers, sets, or triangles or any other coextensive subject matter — in fact, they aren't "about" anything at all. Rather, mathematical statements are syntactic forms whose shapes and locations have no meaning unless they are given an interpretation. In contrast to mathematical realism, logicism, or intuitionism, formalism's contours are less defined due to broad approaches that can be categorized as formalist.
This page is based on this Wikipedia article Text is available under the CC BY-SA 4.0 license; additional terms may apply. Images, videos and audio are available under their respective licenses.
