Stratified randomization

Last updated
Graphic breakdown of stratified random sampling StratifiedRandomSampling.jpg
Graphic breakdown of stratified random sampling

In statistics, stratified randomization is a method of sampling which first stratifies the whole study population into subgroups with same attributes or characteristics, known as strata, then followed by simple random sampling from the stratified groups, where each element within the same subgroup are selected unbiasedly during any stage of the sampling process, randomly and entirely by chance. [1] [2] Stratified randomization is considered a subdivision of stratified sampling, and should be adopted when shared attributes exist partially and vary widely between subgroups of the investigated population, so that they require special considerations or clear distinctions during sampling. [3] This sampling method should be distinguished from cluster sampling, where a simple random sample of several entire clusters is selected to represent the whole population, or stratified systematic sampling, where a systematic sampling is carried out after the stratification process.

Contents

Steps for stratified random sampling

Stratified randomization is extremely useful when the target population is heterogeneous and effectively displays how the trends or characteristics under study differ between strata. [1] When performing a stratified randomization, the following 8 steps should be taken: [4]

  1. Define a target population.
  2. Define stratification variables and decide the number of strata to be created. The criteria for defining variables for stratification include age, socioeconomic status, nationality, race, education level and others and should be in line with the research objective. Ideally, 4-6 strata should be employed, as any increase in stratification variables will raise the probability for some of them to cancel out the impact of other variables.
  3. Use a sampling frame to evaluate all the elements in the target population. Make changes afterwards based on coverage and grouping.
  4. List all the elements and consider the sampling result. Each stratum should be mutually exclusive and add up to cover all members of the population, whilst each member of the population should fall into unique stratum, along with other members with minimum differences. [4]
  5. Make decisions over the random sampling selection criteria. This can be done manually or with a designed computer program.
  6. Assign a random and unique number to all the elements followed by sorting these elements according to their number assigned.
  7. Review the size of each stratum and numerical distribution of all elements in every strata. Determine the type of sampling, either proportional or disproportional stratified sampling.
  8. Carry out the selected random sampling as defined in step 5. At minimum, one element must be chosen from each stratum so that the final sample includes representatives from every stratum. If two or more elements from each stratum are selected, error margins of the collected data can be calculated.

Stratified random assignment

Stratified randomization may also refer to the random assignment of treatments to subjects, in addition to referring to random sampling of subjects from a population, as described above.

Simple random sampling after stratification step Stratified sampling.PNG
Simple random sampling after stratification step

In this context, stratified randomization uses one or multiple prognostic factors to make subgroups, on average, that have similar entry characteristics. The patient factor can be accurately decided by examining the outcome in previous studies. [5]

The number of subgroups can be calculated by multiplying the number of strata for each factor.  Factors are measured before or at the time of randomization and experimental subjects are divided into several subgroups or strata according to the results of measurements. [6]

Within each stratum, several randomization strategies can be applied, which involves simple randomization, blocked randomization, and minimization.

Simple randomization within strata

Simple randomization is considered as the easiest method for allocating subjects in each stratum. Subjects are assigned to each group purely randomly for every assignment. Even though it is easy to conduct, simple randomization is commonly applied in strata that contain more than 100 samples since a small sampling size would make assignment unequal. [6]

Block randomization within strata

Block randomization, sometimes called permuted block randomization, applies blocks to allocate subjects from the same strata equally to each group in the study. In block randomization, allocation ratio (ratio of the number of one specific group over other groups) and group sizes are specified. The block size must be the multiples of the number of treatments so that samples in each stratum can be assigned to treatment groups with the intended ratio. [6] For instance, there should be 4 or 8 strata in a clinical trial concerning breast cancer where age and nodal statuses are two prognostic factors and each factor is split into two-level. The different blocks can be assigned to samples in multiple ways including random list and computer programming. [7] [8]

Block randomization is commonly used in the experiment with a relatively big sampling size to avoid the imbalance allocation of samples with important characteristics. In certain fields with strict requests of randomization such as clinical trials, the allocation would be predictable when there is no blinding process for conductors and the block size is limited. The blocks permuted randomization in strata could possibly cause an imbalance of samples among strata as the number of strata increases and the sample size is limited, For instance, there is a possibility that no sample is found meeting the characteristic of certain strata. [9]

Minimization method

In order to guarantee the similarity of each treatment group, the "minimization" method attempts are made, which is more direct than random permuted block within strats. In the minimization method, samples in each stratum are assigned to treatment groups based on the sum of samples in each treatment group, which makes the number of subjects keep balance among the group. [6] If the sums for multiple treatment groups are the same, simple randomization would be conducted to assign the treatment. In practice, the minimization method needs to follow a daily record of treatment assignments by prognostic factors, which can be done effectively by using a set of index cards to record.  The minimization method effectively avoids imbalance among groups but involves less random process than block randomization because the random process is only conducted when the treatment sums are the same. A feasible solution is to apply an additional random list which makes the treatment groups with a smaller sum of marginal totals possess a higher chance (e.g.¾) while other treatments have a lower chance(e.g.¼ ). [10]

Application

Confounding factors are important to consider in clinical trials Assessing the role of a confounder.png
Confounding factors are important to consider in clinical trials

Stratified random sampling is useful and productive in situations requiring different weightings on specific strata. In this way, the researchers can manipulate the selection mechanisms from each strata to amplify or minimize the desired characteristics in the survey result. [11]

Stratified randomization is helpful when researchers intend to seek for associations between two or more strata, as simple random sampling causes a larger chance of unequal representation of target groups. It is also useful when the researchers wish to eliminate confounders in observational studies as stratified random sampling allows the adjustments of covariances and the p-values for more accurate results. [12]

There is also a higher level of statistical accuracy for stratified random sampling compared with simple random sampling, due to the high relevance of elements chosen to represent the population. The differences within the strata is much less compared to the one between strata. Hence, as the between-sample differences are minimized, the standard deviation will be consequently tightened, resulting in higher degree of accuracy and small error in the final results. This effectively reduces the sample size needed and increases cost-effectiveness of sampling when research funding is tight.

In real life, stratified random sampling can be applied to results of election polling, investigations into income disparities among social groups, or measurements of education opportunities across nations. [1]

Stratified randomization in clinical trials

In clinical trials, patients are stratified according to their social and individual backgrounds, or any factor that are relevant to the study, to match each of these groups within the entire patient population. The aim of such is to create a balance of clinical/prognostic factor as the trials would not produce valid results if the study design is not balanced. [13] The step of stratified randomization is extremely important as an attempt to ensure that no bias, deliberate or accidental, affects the representative nature of the patient sample under study. [14] It increases the study power, especially in small clinical trials(n<400), as these known clinical traits stratified are thought to effect the outcomes of the interventions. [15] It helps prevent the occurrence of type I error, which is valued highly in clinical studies. [16] It also has an important effect on sample size for active control equivalence trials and in theory, facilitates subgroup analysis and interim analysis. [16]

Advantage

The advantages of stratified randomization include:

  1. Stratified randomization can accurately reflect the outcomes of the general population since influential factors are applied to stratify the entire samples and balance the samples' vital characteristics among treatment groups. For instance, applying stratified randomization to make a sample of 100 from the population can guarantee the balance of males and females in each treatment group, while using simple randomization might result in only 20 males in one group and 80 males in another group. [6]
  2. Stratified randomization can have lower variance than other sampling methods such as cluster sampling, simple random sampling, and systematic sampling or non-probability methods since measurements within strata could be made to have a lower standard deviation. Randomizing divided strata are more manageable and cheaper in some cases than simply randomizing general samples. [10]
  3. It is easier for a team to be trained to stratify a sample because of the exactness of the nature of stratified randomization. [6]
  4. Sometimes stratified randomization is desirable to have estimates of population parameters for groups within the population. [10]

Disadvantage

The limits of stratified randomization include:

  1. Stratified randomization firstly divides samples into several strata with reference to prognostic factors but there is possible that the samples are unable to be divided. In application, the significance of prognostic factors lacks strict approval in some cases, which could further result in bias. This is why the factors' potential for making effects to result should be checked before the factors are included in stratification. In some cases that the impact of factors on the outcome cannot be approved, unstratified randomization is suggested. [17]
  2. The subgroup size is taken to be of the same importance if the data available cannot represent overall subgroup population. In some applications, subgroup size is decided with reference to the amount of data available instead of scaling sample sizes to subgroup size, which would introduce bias in the effects of factors.  In some cases that data needs to be stratified by variances, subgroup variances differ significantly, making each subgroup sampling size proportional to the overall subgroup population cannot be guaranteed. [18]
  3. Will perform worse than other methods if the stratums aren’t chosen smartly. In particular this happens if the within strata variance is high.
  4. The process of assigning samples into subgroups could involve overlapping if subjects meet the inclusion standard of multiple strata, which could result in a misrepresentation of the population. [18]

See also

Related Research Articles

Analysis of variance (ANOVA) is a collection of statistical models and their associated estimation procedures used to analyze the differences among means. ANOVA was developed by the statistician Ronald Fisher. ANOVA is based on the law of total variance, where the observed variance in a particular variable is partitioned into components attributable to different sources of variation. In its simplest form, ANOVA provides a statistical test of whether two or more population means are equal, and therefore generalizes the t-test beyond two means. In other words, the ANOVA is used to test the difference between two or more means.

<span class="mw-page-title-main">Cluster sampling</span> Sampling methodology in statistics

In statistics, cluster sampling is a sampling plan used when mutually homogeneous yet internally heterogeneous groupings are evident in a statistical population. It is often used in marketing research.

In statistics, survey sampling describes the process of selecting a sample of elements from a target population to conduct a survey. The term "survey" may refer to many different types or techniques of observation. In survey sampling it most often involves a questionnaire used to measure the characteristics and/or attitudes of people. Different ways of contacting members of a sample once they have been selected is the subject of survey data collection. The purpose of sampling is to reduce the cost and/or the amount of work that it would take to survey the entire target population. A survey that measures the entire target population is called a census. A sample refers to a group or section of a population from which information is to be obtained.

<span class="mw-page-title-main">Stratified sampling</span> Sampling from a population which can be partitioned into subpopulations

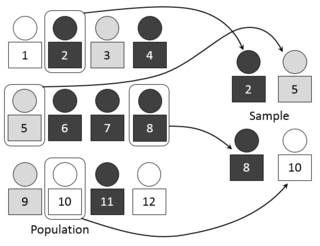
In statistics, stratified sampling is a method of sampling from a population which can be partitioned into subpopulations.

Randomization is a statistical process in which a random mechanism is employed to select a sample from a population or assign subjects to different groups. The process is crucial in ensuring the random allocation of experimental units or treatment protocols, thereby minimizing selection bias and enhancing the statistical validity. It facilitates the objective comparison of treatment effects in experimental design, as it equates groups statistically by balancing both known and unknown factors at the outset of the study. In statistical terms, it underpins the principle of probabilistic equivalence among groups, allowing for the unbiased estimation of treatment effects and the generalizability of conclusions drawn from sample data to the broader population.

In statistics, multistage sampling is the taking of samples in stages using smaller and smaller sampling units at each stage.

<span class="mw-page-title-main">Sampling (statistics)</span> Selection of data points in statistics.

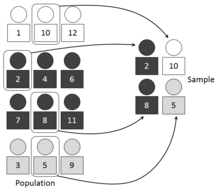
In statistics, quality assurance, and survey methodology, sampling is the selection of a subset or a statistical sample of individuals from within a statistical population to estimate characteristics of the whole population. The subset is meant to reflect the whole population and statisticians attempt to collect samples that are representative of the population. Sampling has lower costs and faster data collection compared to recording data from the entire population, and thus, it can provide insights in cases where it is infeasible to measure an entire population.

<span class="mw-page-title-main">Randomized controlled trial</span> Form of scientific experiment

A randomized controlled trial is a form of scientific experiment used to control factors not under direct experimental control. Examples of RCTs are clinical trials that compare the effects of drugs, surgical techniques, medical devices, diagnostic procedures, diets or other medical treatments.

Stratification may refer to:

In the design of experiments, hypotheses are applied to experimental units in a treatment group. In comparative experiments, members of a control group receive a standard treatment, a placebo, or no treatment at all. There may be more than one treatment group, more than one control group, or both.

Sample size determination or estimation is the act of choosing the number of observations or replicates to include in a statistical sample. The sample size is an important feature of any empirical study in which the goal is to make inferences about a population from a sample. In practice, the sample size used in a study is usually determined based on the cost, time, or convenience of collecting the data, and the need for it to offer sufficient statistical power. In complex studies, different sample sizes may be allocated, such as in stratified surveys or experimental designs with multiple treatment groups. In a census, data is sought for an entire population, hence the intended sample size is equal to the population. In experimental design, where a study may be divided into different treatment groups, there may be different sample sizes for each group.

A stratum in geology is a layer of sedimentary rock or sediment. In archaeology, it is a layer of man-produced sediment of a certain age.

<span class="mw-page-title-main">Confounding</span> Variable or factor in causal inference

In causal inference, a confounder is a variable that influences both the dependent variable and independent variable, causing a spurious association. Confounding is a causal concept, and as such, cannot be described in terms of correlations or associations. The existence of confounders is an important quantitative explanation why correlation does not imply causation. Some notations are explicitly designed to identify the existence, possible existence, or non-existence of confounders in causal relationships between elements of a system.

Minimisation is a method of adaptive stratified sampling that is used in clinical trials, as described by Pocock and Simon.

Balanced repeated replication is a statistical technique for estimating the sampling variability of a statistic obtained by stratified sampling.

Stratification of clinical trials is the partitioning of subjects and results by a factor other than the treatment given.

In mathematics, especially in topology, a stratified space is a topological space that admits or is equipped with a stratification, a decomposition into subspaces, which are nice in some sense.

In survey research, the design effect is a number that shows how well a sample of people may represent a larger group of people for a specific measure of interest. This is important when the sample comes from a sampling method that is different than just picking people using a simple random sample.

Principal stratification is a statistical technique used in causal inference when adjusting results for post-treatment covariates. The idea is to identify underlying strata and then compute causal effects only within strata. It is a generalization of the local average treatment effect (LATE) in the sense of presenting applications besides all-or-none compliance. The LATE method, which was independently developed by Imbens and Angrist (1994) and Baker and Lindeman (1994) also included the key exclusion restriction and monotonicity assumptions for identifiability. For the history of early developments see Baker, Kramer, Lindeman.

In statistics, the Cochran–Mantel–Haenszel test (CMH) is a test used in the analysis of stratified or matched categorical data. It allows an investigator to test the association between a binary predictor or treatment and a binary outcome such as case or control status while taking into account the stratification. Unlike the McNemar test, which can only handle pairs, the CMH test handles arbitrary strata sizes. It is named after William G. Cochran, Nathan Mantel and William Haenszel. Extensions of this test to a categorical response and/or to several groups are commonly called Cochran–Mantel–Haenszel statistics. It is often used in observational studies in which random assignment of subjects to different treatments cannot be controlled but confounding covariates can be measured.

References

  1. 1 2 3 Nickolas, Steven (July 14, 2019). "How Stratified Random Sampling Works". Investopedia. Retrieved 2020-04-07.
  2. ↑ "Simple random sample", Wikipedia, 2020-03-18, retrieved 2020-04-07
  3. ↑ "Stratified sampling", Wikipedia, 2020-02-09, retrieved 2020-04-07
  4. 1 2 Stephanie (Dec 11, 2013). "Stratified Random Sample: Definition, Examples". Statistics How To. Retrieved 2020-04-07.
  5. ↑ Sylvester, Richard (December 1982). "Fundamentals of clinical trials". Controlled Clinical Trials. 3 (4): 385–386. doi:10.1016/0197-2456(82)90029-0. ISSN   0197-2456.
  6. 1 2 3 4 5 6 Pocock, Stuart J. (Jul 1, 2013). Clinical trials : a practical approach. Chichester: John Wiley & Sons Ltd. ISBN   978-1-118-79391-6. OCLC   894581169.
  7. ↑ "Sealed Envelope | Random permuted blocks". www.sealedenvelope.com. Feb 25, 2020. Retrieved 2020-04-07.
  8. ↑ Friedman, Lawrence M.; Furberg, Curt D.; DeMets, David L. (2010), "Introduction to Clinical Trials", Fundamentals of Clinical Trials, Springer New York, pp. 1–18, doi:10.1007/978-1-4419-1586-3_1, ISBN   978-1-4419-1585-6
  9. ↑ Fundamentals of clinical trials. Friedman, Lawrence M., 1942-, Furberg, Curt,, DeMets, David L., 1944-, Reboussin, David,, Granger, Christopher B. (Fifth ed.). New York. 27 August 2015. ISBN   978-3-319-18539-2. OCLC   919463985.{{cite book}}: CS1 maint: location missing publisher (link) CS1 maint: others (link)
  10. 1 2 3 Pocock, S. J. (March 1979). "Allocation of Patients to Treatment in Clinical Trials". Biometrics. 35 (1): 183–197. doi:10.2307/2529944. ISSN   0006-341X. JSTOR   2529944. PMID   497334.
  11. ↑ Crossman, Ashley (Jan 27, 2020). "Understanding Stratified Samples and How to Make Them". ThoughtCo. Retrieved 2020-04-07.
  12. ↑ Hennekens, Charles H. (1987). Epidemiology in medicine. Buring, Julie E., Mayrent, Sherry L. (1st ed.). Boston, Massachusetts: Little, Brown. ISBN   0-316-35636-0. OCLC   16890223.
  13. ↑ Polit, DF; Beck, CT (2012). Nursing Research: Generating and Assessing Evidence for Nursing Practice, 9th ed. Philadelphia, USA: Wolters Klower Health: Lippincott Williams & Wilkins.
  14. ↑ "Patient Stratification in Clinical Trials". Omixon | NGS for HLA. 2014-12-01. Retrieved 2020-04-26.
  15. ↑ Stephanie (2016-05-20). "Stratified Randomization in Clinical Trials". Statistics How To. Retrieved 2020-04-26.
  16. 1 2 Kernan, W (Jan 1999). "Stratified Randomization for Clinical Trials". Journal of Clinical Epidemiology. 52 (1): 19–26. doi: 10.1016/S0895-4356(98)00138-3 . PMID   9973070.
  17. ↑ Murphy, Chris B. (Apr 13, 2019). "Pros and Cons of Stratified Random Sampling". Investopedia. Retrieved 2020-04-07.
  18. 1 2 Glass, Aenne; Kundt, Guenther (2014), Potential Advantages and Disadvantages of Stratification in Methods of Randomization, Springer Proceedings in Mathematics & Statistics, vol. 114, Springer New York, pp. 239–246, doi:10.1007/978-1-4939-2104-1_23, ISBN   978-1-4939-2103-4
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.