In mathematics, the Leech lattice is an even unimodular lattice Λ24 in 24-dimensional Euclidean space, which is one of the best models for the kissing number problem. It was discovered by John Leech. It may also have been discovered by Ernst Witt in 1940.

In geometry, a sphere packing is an arrangement of non-overlapping spheres within a containing space. The spheres considered are usually all of identical size, and the space is usually three-dimensional Euclidean space. However, sphere packing problems can be generalised to consider unequal spheres, spaces of other dimensions or to non-Euclidean spaces such as hyperbolic space.

In mathematics, a Hadamard matrix, named after the French mathematician Jacques Hadamard, is a square matrix whose entries are either +1 or −1 and whose rows are mutually orthogonal. In geometric terms, this means that each pair of rows in a Hadamard matrix represents two perpendicular vectors, while in combinatorial terms, it means that each pair of rows has matching entries in exactly half of their columns and mismatched entries in the remaining columns. It is a consequence of this definition that the corresponding properties hold for columns as well as rows.
The theory of association schemes arose in statistics, in the theory of experimental design for the analysis of variance. In mathematics, association schemes belong to both algebra and combinatorics. In algebraic combinatorics, association schemes provide a unified approach to many topics, for example combinatorial designs and the theory of error-correcting codes. In algebra, association schemes generalize groups, and the theory of association schemes generalizes the character theory of linear representations of groups.
In geometry, a set of lines is called equiangular if all the lines intersect at a single point, and every pair of lines makes the same angle.
Vladimir Iosifovich Levenshtein was a Russian and Soviet scientist who did research in information theory, error-correcting codes, and combinatorial design. Among other contributions, he is known for the Levenshtein distance and a Levenshtein algorithm, which he developed in 1965.
In mathematics, a conference matrix (also called a C-matrix) is a square matrix C with 0 on the diagonal and +1 and −1 off the diagonal, such that CTC is a multiple of the identity matrix I. Thus, if the matrix has order n, CTC = (n−1)I. Some authors use a more general definition, which requires there to be a single 0 in each row and column but not necessarily on the diagonal.
In mathematics, Dvoretzky's theorem is an important structural theorem about normed vector spaces proved by Aryeh Dvoretzky in the early 1960s, answering a question of Alexander Grothendieck. In essence, it says that every sufficiently high-dimensional normed vector space will have low-dimensional subspaces that are approximately Euclidean. Equivalently, every high-dimensional bounded symmetric convex set has low-dimensional sections that are approximately ellipsoids.
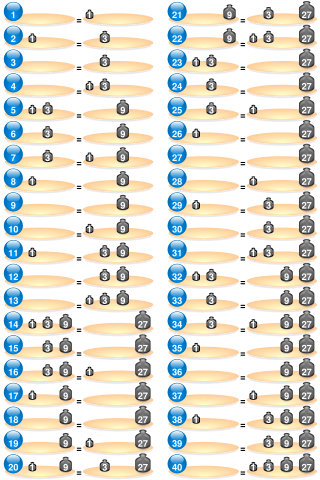
In mathematics, a power of three is a number of the form 3n where n is an integer, that is, the result of exponentiation with number three as the base and integer n as the exponent.
Polyhedral combinatorics is a branch of mathematics, within combinatorics and discrete geometry, that studies the problems of counting and describing the faces of convex polyhedra and higher-dimensional convex polytopes.

In the context of quantum mechanics and quantum information theory, symmetric, informationally complete, positive operator-valued measures (SIC-POVMs) are a particular type of generalized measurement (POVM). SIC-POVMs are particularly notable thanks to their defining features of (1) being informationally complete; (2)having the minimal number of outcomes compatible with informational completeness, and (3) being highly symmetric. In this context, informational completeness is the property of a POVM of allowing to fully reconstruct input states from measurement data.
A quantum t-design is a probability distribution over either pure quantum states or unitary operators which can duplicate properties of the probability distribution over the Haar measure for polynomials of degree t or less. Specifically, the average of any polynomial function of degree t over the design is exactly the same as the average over Haar measure. Here the Haar measure is a uniform probability distribution over all quantum states or over all unitary operators. Quantum t-designs are so called because they are analogous to t-designs in classical statistics, which arose historically in connection with the problem of design of experiments. Two particularly important types of t-designs in quantum mechanics are projective and unitary t-designs.
In mathematics, a Bose–Mesner algebra is a special set of matrices which arise from a combinatorial structure known as an association scheme, together with the usual set of rules for combining those matrices, such that they form an associative algebra, or, more precisely, a unitary commutative algebra. Among these rules are:
Thomas Zaslavsky is an American mathematician specializing in combinatorics.
Mathematics is a broad subject that is commonly divided in many areas that may be defined by their objects of study, by the used methods, or by both. For example, analytic number theory is a subarea of number theory devoted to the use of methods of analysis for the study of natural numbers.

Asymptotic safety is a concept in quantum field theory which aims at finding a consistent and predictive quantum theory of the gravitational field. Its key ingredient is a nontrivial fixed point of the theory's renormalization group flow which controls the behavior of the coupling constants in the ultraviolet (UV) regime and renders physical quantities safe from divergences. Although originally proposed by Steven Weinberg to find a theory of quantum gravity, the idea of a nontrivial fixed point providing a possible UV completion can be applied also to other field theories, in particular to perturbatively nonrenormalizable ones. In this respect, it is similar to quantum triviality.
In mathematics, the upper bound theorem states that cyclic polytopes have the largest possible number of faces among all convex polytopes with a given dimension and number of vertices. It is one of the central results of polyhedral combinatorics.

Maryna Sergiivna Viazovska is a Ukrainian mathematician known for her work in sphere packing. She is a full professor and Chair of Number Theory at the Institute of Mathematics of the École Polytechnique Fédérale de Lausanne in Switzerland. She was awarded the Fields Medal in 2022.
In physics, the poppy-seed bagel theorem concerns interacting particles confined to a bounded surface when the particles repel each other pairwise with a magnitude that is proportional to the inverse distance between them raised to some positive power . In particular, this includes the Coulomb law observed in Electrostatics and Riesz potentials extensively studied in Potential theory. Other classes of potentials, which not necessarily involve the Riesz kernel, for example nearest neighbor interactions, are also described by this theorem in the macroscopic regime. For such particles, a stable equilibrium state, which depends on the parameter , is attained when the associated potential energy of the system is minimal. For large numbers of points, these equilibrium configurations provide a discretization of which may or may not be nearly uniform with respect to the surface area of . The poppy-seed bagel theorem asserts that for a large class of sets , the uniformity property holds when the parameter is larger than or equal to the dimension of the set . For example, when the points are confined to the 2-dimensional surface of a torus embedded in 3 dimensions, one can create a large number of points that are nearly uniformly spread on the surface by imposing a repulsion proportional to the inverse square distance between the points, or any stronger repulsion. From a culinary perspective, to create the nearly perfect poppy-seed bagel where bites of equal size anywhere on the bagel would contain essentially the same number of poppy seeds, impose at least an inverse square distance repelling force on the seeds.
In graph theory, the Games graph is the largest known locally linear strongly regular graph. Its parameters as a strongly regular graph are (729,112,1,20). This means that it has 729 vertices, and 40824 edges. Each edge is in a unique triangle and each non-adjacent pair of vertices have exactly 20 shared neighbors. It is named after Richard A. Games, who suggested its construction in an unpublished communication and wrote about related constructions.







