 | This article has multiple issues. Please help improve it or discuss these issues on the talk page . (Learn how and when to remove these template messages)
|
In statistics, a unit is one member of a set of entities being studied. It is the main source for the mathematical abstraction of a "random variable". Common examples of a unit would be a single person, animal, plant, manufactured item, or country that belongs to a larger collection of such entities being studied.
Units are often referred to as being either experimental units or sampling units:
For example, in an experiment on educational methods, methods may be applied to classrooms of students. This would make the classroom as the experimental unit. Measurements of progress may be obtained from individual students, as observational units. But the treatment (teaching method) being applied to the class would not be applied independently to the individual students. Hence, the student could not be regarded as the experimental unit. The class, or the teacher (who applies the method, if he/she has multiple classes), would be the appropriate experimental unit.
In most statistical studies, the goal is to generalize from the observed units to a larger set consisting of all comparable units that exist but are not directly observed. For example, if we randomly sample 100 people and ask them which candidate they intend to vote for in an election, our main interest is in the voting behavior of all eligible voters, not exclusively on the 100 observed units.
In some cases, the observed units may not form a sample from any meaningful population, but rather constitute a convenience sample, or may represent the entire population of interest. In this situation, we may study the units descriptively, or we may study their dynamics over time. But it typically does not make sense to talk about generalizing to a larger population of such units. Studies involving countries or business firms are often of this type. Clinical trials also typically use convenience samples, however the aim is often to make inferences about the effectiveness of treatments in other patients, and given the inclusion and exclusion criteria for some clinical trials, the sample may not be representative of the majority of patients with the condition or disease.
In simple data sets, the units are in one-to-one correspondence with the data values. In more complex data sets, multiple measurements are made for each unit. For example, if blood pressure measurements are made daily for a week on each subject in a study, there would be seven data values for each statistical unit. Multiple measurements taken on an individual are not independent (they will be more alike compared to measurements taken on different individuals). Ignoring these dependencies, the analysis can lead to an inflated sample size or pseudoreplication.
While a unit is often the lowest level at which observations are made, in some cases, a unit can be further decomposed as a statistical assembly.
Many statistical analyses use quantitative data that have units of measurement. This is a distinct and non-overlapping use of the term "unit."
Statistical units are divided into two types. They are:
{{cite book}}: CS1 maint: multiple names: authors list (link)| Scientific method | |
|---|---|
| Treatment and blocking | |
| Models and inference | |
| Designs Completely randomized | |
Analysis of variance (ANOVA) is a collection of statistical models and their associated estimation procedures used to analyze the differences among means. ANOVA was developed by the statistician Ronald Fisher. ANOVA is based on the law of total variance, where the observed variance in a particular variable is partitioned into components attributable to different sources of variation. In its simplest form, ANOVA provides a statistical test of whether two or more population means are equal, and therefore generalizes the t-test beyond two means. In other words, the ANOVA is used to test the difference between two or more means.
The design of experiments, also known as experiment design or experimental design, is the design of any task that aims to describe and explain the variation of information under conditions that are hypothesized to reflect the variation. The term is generally associated with experiments in which the design introduces conditions that directly affect the variation, but may also refer to the design of quasi-experiments, in which natural conditions that influence the variation are selected for observation.
Econometrics is an application of statistical methods to economic data in order to give empirical content to economic relationships. More precisely, it is "the quantitative analysis of actual economic phenomena based on the concurrent development of theory and observation, related by appropriate methods of inference." An introductory economics textbook describes econometrics as allowing economists "to sift through mountains of data to extract simple relationships." Jan Tinbergen is one of the two founding fathers of econometrics. The other, Ragnar Frisch, also coined the term in the sense in which it is used today.
Multivariate statistics is a subdivision of statistics encompassing the simultaneous observation and analysis of more than one outcome variable, i.e., multivariate random variables. Multivariate statistics concerns understanding the different aims and background of each of the different forms of multivariate analysis, and how they relate to each other. The practical application of multivariate statistics to a particular problem may involve several types of univariate and multivariate analyses in order to understand the relationships between variables and their relevance to the problem being studied.
Statistics is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of surveys and experiments.
Statistical inference is the process of using data analysis to infer properties of an underlying distribution of probability. Inferential statistical analysis infers properties of a population, for example by testing hypotheses and deriving estimates. It is assumed that the observed data set is sampled from a larger population.
An experiment is a procedure carried out to support or refute a hypothesis, or determine the efficacy or likelihood of something previously untried. Experiments provide insight into cause-and-effect by demonstrating what outcome occurs when a particular factor is manipulated. Experiments vary greatly in goal and scale but always rely on repeatable procedure and logical analysis of the results. There also exist natural experimental studies.
Randomization is a statistical process in which a random mechanism is employed to select a sample from a population or assign subjects to different groups. The process is crucial in ensuring the random allocation of experimental units or treatment protocols, thereby minimizing selection bias and enhancing the statistical validity. It facilitates the objective comparison of treatment effects in experimental design, as it equates groups statistically by balancing both known and unknown factors at the outset of the study. In statistical terms, it underpins the principle of probabilistic equivalence among groups, allowing for the unbiased estimation of treatment effects and the generalizability of conclusions drawn from sample data to the broader population.
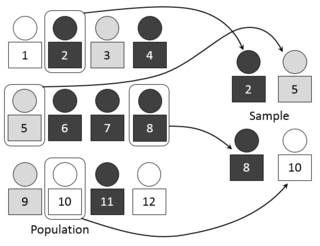
In statistics, quality assurance, and survey methodology, sampling is the selection of a subset or a statistical sample of individuals from within a statistical population to estimate characteristics of the whole population. The subset is meant to reflect the whole population and statisticians attempt to collect samples that are representative of the population. Sampling has lower costs and faster data collection compared to recording data from the entire population, and thus, it can provide insights in cases where it is infeasible to measure an entire population.
Quantitative marketing research is the application of quantitative research techniques to the field of marketing research. It has roots in both the positivist view of the world, and the modern marketing viewpoint that marketing is an interactive process in which both the buyer and seller reach a satisfying agreement on the "four Ps" of marketing: Product, Price, Place (location) and Promotion.
Experimental psychology refers to work done by those who apply experimental methods to psychological study and the underlying processes. Experimental psychologists employ human participants and animal subjects to study a great many topics, including sensation, perception, memory, cognition, learning, motivation, emotion; developmental processes, social psychology, and the neural substrates of all of these.
In statistics, an interaction may arise when considering the relationship among three or more variables, and describes a situation in which the effect of one causal variable on an outcome depends on the state of a second causal variable. Although commonly thought of in terms of causal relationships, the concept of an interaction can also describe non-causal associations. Interactions are often considered in the context of regression analyses or factorial experiments.
External validity is the validity of applying the conclusions of a scientific study outside the context of that study. In other words, it is the extent to which the results of a study can generalize or transport to other situations, people, stimuli, and times. Generalizability refers to the applicability of a predefined sample to a broader population while transportability refers to the applicability of one sample to another target population. In contrast, internal validity is the validity of conclusions drawn within the context of a particular study.
This glossary of statistics and probability is a list of definitions of terms and concepts used in the mathematical sciences of statistics and probability, their sub-disciplines, and related fields. For additional related terms, see Glossary of mathematics and Glossary of experimental design.
Spatial analysis is any of the formal techniques which studies entities using their topological, geometric, or geographic properties. Spatial analysis includes a variety of techniques using different analytic approaches, especially spatial statistics. It may be applied in fields as diverse as astronomy, with its studies of the placement of galaxies in the cosmos, or to chip fabrication engineering, with its use of "place and route" algorithms to build complex wiring structures. In a more restricted sense, spatial analysis is geospatial analysis, the technique applied to structures at the human scale, most notably in the analysis of geographic data. It may also be applied to genomics, as in transcriptomics data.
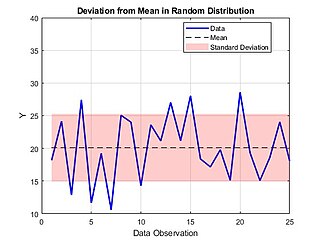
In mathematics and statistics, deviation serves as a measure to quantify the disparity between an observed value of a variable and another designated value, frequently the mean of that variable. Deviations with respect to the sample mean and the population mean are called errors and residuals, respectively. The sign of the deviation reports the direction of that difference: the deviation is positive when the observed value exceeds the reference value. The absolute value of the deviation indicates the size or magnitude of the difference. In a given sample, there are as many deviations as sample points. Summary statistics can be derived from a set of deviations, such as the standard deviation and the mean absolute deviation, measures of dispersion, and the mean signed deviation, a measure of bias.
In statistics, the multiple comparisons, multiplicity or multiple testing problem occurs when one considers a set of statistical inferences simultaneously or estimates a subset of parameters selected based on the observed values.
In engineering, science, and statistics, replication is the process of repeating a study or experiment under the same or similar conditions to support the original claim, which crucial to confirm the accuracy of results as well as for identifying and correcting the flaws in the original experiment. ASTM, in standard E1847, defines replication as "... the repetition of the set of all the treatment combinations to be compared in an experiment. Each of the repetitions is called a replicate."
A quasi-experiment is an empirical interventional study used to estimate the causal impact of an intervention on target population without random assignment. Quasi-experimental research shares similarities with the traditional experimental design or randomized controlled trial, but it specifically lacks the element of random assignment to treatment or control. Instead, quasi-experimental designs typically allow the researcher to control the assignment to the treatment condition, but using some criterion other than random assignment.
A glossary of terms used in experimental research.
