This article needs additional citations for verification .(October 2008) |
The following is a timeline of probability and statistics.
This article needs additional citations for verification .(October 2008) |
The following is a timeline of probability and statistics.
Bayesian probability is an interpretation of the concept of probability, in which, instead of frequency or propensity of some phenomenon, probability is interpreted as reasonable expectation representing a state of knowledge or as quantification of a personal belief.

Frequentist probability or frequentism is an interpretation of probability; it defines an event's probability as the limit of its relative frequency in many trials. Probabilities can be found by a repeatable objective process. The continued use of frequentist methods in scientific inference, however, has been called into question.

Probability is the branch of mathematics concerning numerical descriptions of how likely an event is to occur, or how likely it is that a proposition is true. The probability of an event is a number between 0 and 1, where, roughly speaking, 0 indicates impossibility of the event and 1 indicates certainty. The higher the probability of an event, the more likely it is that the event will occur. A simple example is the tossing of a fair (unbiased) coin. Since the coin is fair, the two outcomes are both equally probable; the probability of 'heads' equals the probability of 'tails'; and since no other outcomes are possible, the probability of either 'heads' or 'tails' is 1/2.

Statistics is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of surveys and experiments.

Statistical inference is the process of using data analysis to infer properties of an underlying distribution of probability. Inferential statistical analysis infers properties of a population, for example by testing hypotheses and deriving estimates. It is assumed that the observed data set is sampled from a larger population.
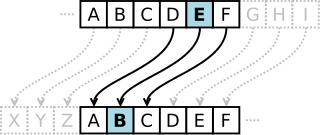
In cryptography, a Caesar cipher, also known as Caesar's cipher, the shift cipher, Caesar's code, or Caesar shift, is one of the simplest and most widely known encryption techniques. It is a type of substitution cipher in which each letter in the plaintext is replaced by a letter some fixed number of positions down the alphabet. For example, with a left shift of 3, D would be replaced by A, E would become B, and so on. The method is named after Julius Caesar, who used it in his private correspondence.
Bayesian inference is a method of statistical inference in which Bayes' theorem is used to update the probability for a hypothesis as more evidence or information becomes available. Bayesian inference is an important technique in statistics, and especially in mathematical statistics. Bayesian updating is particularly important in the dynamic analysis of a sequence of data. Bayesian inference has found application in a wide range of activities, including science, engineering, philosophy, medicine, sport, and law. In the philosophy of decision theory, Bayesian inference is closely related to subjective probability, often called "Bayesian probability".

Abraham de Moivre FRS was a French mathematician known for de Moivre's formula, a formula that links complex numbers and trigonometry, and for his work on the normal distribution and probability theory.

The Doctrine of Chances was the first textbook on probability theory, written by 18th-century French mathematician Abraham de Moivre and first published in 1718. De Moivre wrote in English because he resided in England at the time, having fled France to escape the persecution of Huguenots. The book's title came to be synonymous with probability theory, and accordingly the phrase was used in Thomas Bayes' famous posthumous paper An Essay towards solving a Problem in the Doctrine of Chances, wherein a version of Bayes' theorem was first introduced.

Abū Yūsuf Yaʻqūb ibn ʼIsḥāq aṣ-Ṣabbāḥ al-Kindī was an Arab Muslim polymath active as a philosopher, mathematician, physician, and music theorist. Al-Kindi was the first of the Islamic peripatetic philosophers, and is hailed as the "father of Arab philosophy".
Bayesian statistics is a theory in the field of statistics based on the Bayesian interpretation of probability where probability expresses a degree of belief in an event. The degree of belief may be based on prior knowledge about the event, such as the results of previous experiments, or on personal beliefs about the event. This differs from a number of other interpretations of probability, such as the frequentist interpretation that views probability as the limit of the relative frequency of an event after many trials.
The classical definition or interpretation of probability is identified with the works of Jacob Bernoulli and Pierre-Simon Laplace. As stated in Laplace's Théorie analytique des probabilités,
Statistics, in the modern sense of the word, began evolving in the 18th century in response to the novel needs of industrializing sovereign states.

Ars Conjectandi is a book on combinatorics and mathematical probability written by Jacob Bernoulli and published in 1713, eight years after his death, by his nephew, Niklaus Bernoulli. The seminal work consolidated, apart from many combinatorial topics, many central ideas in probability theory, such as the very first version of the law of large numbers: indeed, it is widely regarded as the founding work of that subject. It also addressed problems that today are classified in the twelvefold way and added to the subjects; consequently, it has been dubbed an important historical landmark in not only probability but all combinatorics by a plethora of mathematical historians. The importance of this early work had a large impact on both contemporary and later mathematicians; for example, Abraham de Moivre.
This is a timeline of pure and applied mathematics history. It is divided here into three stages, corresponding to stages in the development of mathematical notation: a "rhetorical" stage in which calculations are described purely by words, a "syncopated" stage in which quantities and common algebraic operations are beginning to be represented by symbolic abbreviations, and finally a "symbolic" stage, in which comprehensive notational systems for formulas are the norm.
Probability has a dual aspect: on the one hand the likelihood of hypotheses given the evidence for them, and on the other hand the behavior of stochastic processes such as the throwing of dice or coins. The study of the former is historically older in, for example, the law of evidence, while the mathematical treatment of dice began with the work of Cardano, Pascal, Fermat and Christiaan Huygens between the 16th and 17th century.
Essay d'analyse sur les jeux de hazard is a book on combinatorics and mathematical probability written by Pierre Remond de Montmort and published in 1708. The work applied ideas from combinatorics and probability to analyse various games of chances popular during the time. This book was mainly influenced by Christiaan Huygens' treatise De ratiociniis in ludo aleae and the knowledge of the fact that Jakob Bernoulli had written an unfinished work in probability. The work was intended to re-create the yet unpublished work of Jakob Bernoulli called Ars Conjectandi. The work greatly influenced the thinking of Montmort's contemporary, Abraham De Moivre.